DEFLATE Compression Algorithm
So in the past I have designed products that were capable of plotting collected data as a graphics file for display in the browser. This isn’t currently possible in the JNIOR and it is a feature that could be added to JANOS. It can be useful. I should also mention that JANOS executes Java and serves files out of JAR and ZIP files which generally utilize DEFLATE compression. So we already perform DEFLATE decompression. With a compressor we can add the ability to create/modify JAR and ZIP archives as well as to generate PNG graphics for plots.
The issue with the specifications is that they describe the compression and file formats but do not give you the algorithms. They don’t tell you how to do it. Just what you must do.
Sure often there is reference code or open source projects that you can find. Those often are complete projects and it is difficult to find the precise code in it that you need to understand if you are to implement the core algorithms. Then that code has been optimized and complicated with options over the years that end up obfuscating the structure. And, no, we don’t just absorb 3rd party code into JANOS. That is not the way to maintain a stable embedded environment. Not in my book.
So far this is the case for DEFLATE. I am going to develop the algorithm from scratch so that I fully understand it, know precisely what every statement does, and how the code will perform in the JANOS platform. Maybe more importantly that it will not misbehave and drag JANOS down.
Well I was thinking that I would openly do that here so you can play along. Some approaches to LZ77 have been patented. I have no clue and am not going to spend weeks trying to understand the patent prose. Supposedly the LZ77 implementation associated with DEFLATE is unencumbered. Maybe so. Still I might get creative and cross some line. I am not overly concerned about it but would like to know, at least before getting some sort of legal complaint.
Yeah so… let’s reinvent the wheel. That’s usually how I roll…
If you look into DEFLATE you will be quickly distracted by data structure and Huffman coding. There is some confusing but genius ways of efficiently conveying the Huffman tables and the Huffman coding even seems to be recursively applied. All of that will boggle your mind even before you get to the LZ77 compression at the heart of it all. So, ignore all of that. We will get to it. I am going to start at the heart and build outwards.
LZ77 compression
The compression works by identifying sequences of bytes that occur in the data stream that are repeated later. The repeated sequence is replaced by a short and efficient reference back to the earlier data thereby reducing the size of the overall stream. A 20-year old document by Antaeus Feldspar describes it well by example (my link has since gone bad).
As everything has a limitation, DEFLATE defines a 32KB sliding window which may contain any referenced prior sequence. It just is not feasible to randomly access the entire data set and allow you to reference sequences all the way back to the beginning. This also keeps distances under control allowing only smaller integers to appear in the stream.
It all sounds great but then you realize that in compression you have search that entire 32KB window for matches to the current sequence of bytes each time a new byte is added. Lots of processor cycles are involved and the whole process could take forever. Of course while the decompressor needs to be ready to reference the whole 32KB window a compressor might use a smaller window. That would reduce the effort involved at the cost of compression efficiency. The specifications suggest window and sequence length factors that might be controlled in balancing speed and space efficiency.
It can all get more complex in that the prior sequence can actually overlap the current sequence (as in the example in that document). A further complication comes in if you consider that lazy matching might lead to better compression. A short sequence match might mask a potentially longer match which could have been more beneficial.
So how do I want to proceed here. Some of this reminds me of the fun in creating JANOS’ Regex engine. Hmm…
The Regex engine ends up compiling the expression into one large state machine through which multiple pointers can progress simultaneously. Pointers are advanced as each character is obtained from the data stream. The first pointer (or last depending on the mode) to make it through the whole expression signals a match. If it sounds complicated, it sort of is but at the same time its pretty cool. As far as Regex goes I’ve been able to apply this to almost all of the standard Regex functionality. But JANOS hasn’t implemented every Regex syntax.
For DEFLATE there is somewhat of a similar situation where we want to examine bytes from the data stream one at a time and have the compression algorithm raise its hand when a sequence can be optimally encoded by a [length, distance] pointer. But we want to consider all possibilities and to try to do what leads to the most efficient compression.
I will start by implementing the sliding window as a queue using my standard approach to such things. The size of the queue will be 32K entries or less. In fact, to start out I’ll probably keep it very small. We can enlarge it later when we benchmark the compression algorithm.
Two index pointers will bound the data in the queue. Each new byte will be inserted at the INPTR and that pointer will be incremented and wrapped as required. The oldest byte will be located at the OUTPTR. Once the queue fills we will have to advance the OUTPTR to make room for the next entry. Older data will be dropped and the queue will run at maximum capacity. This is the sliding window.
The sliding window caches the uncompressed data stream. The compressed data stream will be generated by the algorithm separately. We need one more pointer in the sliding widow indicating the start of the current sequence being evaluated. Call that CURPTR. If the current sequence cannot be matched we would output the byte from CURPTR and advance and wrap the pointer as necessary. If the sequence is matched we output the [length, distance] code and advance CURPTR to skip the entire matched sequence.
CURPTR then will lag behind INPTR. It will not get in the way of OUTPTR as DEFLATE specifies a maximum length for the sequence match of 238 bytes and our sliding window will be much larger.
Now lets think about the sequence matching procedure…
I am going to prototype my algorithm in Java on the JNIOR just to make it easier to test and debug. Later, once I have the structure, I can recast it in C and embed it into JANOS.
We’re going to focus on the LZ77 part of the compression first. Our main goal is simply to be compatible with decompression. Our LZ77 algorithm then basically doesn’t have to do anything. We wouldn’t need to find a single repeated sequence nor replace anything with pointers back to any sliding window. Of course our compression ratio wouldn’t be all that impressive. We would still gain through the latter Huffman Coding stages which I am leaving to later. But in the end we would still be able to create file collections and PNG graphics files that are universally usable.
But really, there no fun in a kludge. Let’s see if we can achieve a LZ77 implementation that we can be proud of. Well, at least one that works.
So for development I am going to create a program that will read a selected file compress it using LZ77 into another. I’ll isolate all of the compression effort into one routine and have the outer program report some statistics upon completion.
Here’s our program for testing compression. All of the compression work will be done in do_compress() and this will report the results. At this point we just copy the source file. Yeah, this will be slow. But it will let us examine what we are trying to do more closely than if I went straight to C and use the debugger. In that case I couldn’t really share it with you.
package jtest;
import com.integpg.system.JANOS;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.File;
import java.io.FileReader;
import java.io.FileWriter;
public class Main {
public static void main(String[] args) throws Throwable {
// Requires a test file (use log as default)
String filename = "/jniorsys.log";
if (args.length > 0)
filename = args[0];
// Open the selected file for reading
File src = new File(filename);
long srclen = src.length();
BufferedReader infile = new BufferedReader(new FileReader(src));
if (!infile.ready())
System.exit(1);
// Create an output file
BufferedWriter outfile = new BufferedWriter(new FileWriter("/outfile.dat"));
// perform compression
long timer = JANOS.uptimeMillis();
do_compress(outfile, infile);
timer = JANOS.uptimeMillis() - timer;
// Close files
outfile.close();
infile.close();
// Output statistics
File dest = new File("/outfile.dat");
long destlen = dest.length();
System.out.printf("Processing %.3f seconds.\n", timer/1000.);
System.out.printf("Source %lld bytes.\n", srclen);
System.out.printf("Result %lld bytes.\n", destlen);
System.out.printf("Ratio %.2f%%\n", 100. - (100. * destlen)/srclen);
}
}
This uses my throws Throwable trick to avoid having to worry about try-catch for the time being.
// Our LZ77 compression engine
static void do_compress(BufferedWriter outfile, BufferedReader infile) throws Throwable {
// simply copy at first
while (infile.ready()) {
int ch = infile.read();
outfile.write(ch);
}
}
bruce_dev /> jtest Processing 32.360 seconds. Source 36737 bytes. Result 36737 bytes. Ratio 0.00% bruce_dev /> echo Blah blah blah blah > blah.dat bruce_dev /> cat blah.dat Blah blah blah blah bruce_dev /> jtest blah.dat Processing 0.023 seconds. Source 21 bytes. Result 21 bytes. Ratio 0.00% bruce_dev />
Now back to thinking about the actual compression and matching sequences from a sliding window.
To start let’s implement our sliding window. Recall that I would use a queue for that. You can see here that depending on the window size we will retain the previous so many bytes. New bytes are queued at the INPTR position and when the queue fills we will push the OUTPTR discarding older data.
// Our LZ77 compression engine
static void do_compress(BufferedWriter outfile, BufferedReader infile) throws Throwable {
// create queue (sliding window)
int window = 1024;
byte[] data = new byte[window];
int inptr = 0;
int outptr = 0;
// simply copy at first
while (infile.ready()) {
// obtain next byte
int ch = infile.read();
// matching (cannot yet so just output byte)
outfile.write(ch);
// queue uncompressed data
data[inptr++] = (byte)ch;
if (inptr == window)
inptr = 0;
if (inptr == outptr) {
outptr++;
if (outptr == window)
outptr = 0;
}
}
}
Now for a particular position in the input stream (CURPTR) we want to scan the queue for sequence matches. We could do that by brute force but for a large sliding window that would be very slow. Also there is the concept of a lazy match which if implemented might lead to better compression ratios. So how to approach the matching process?
So for some position the input stream we will be searching prior data for a sequence match (3 or more bytes). So we create the CURPTR. If we cannot find a match (and right now we cannot because we haven’t implemented matching) we will just output the data byte and bump the current position. Searching will continue for a match starting at the new position.
Right now CURPTR will track INTPTR. Later while we are watching for matches it will lag behind. Here we have created CURPTR. There is otherwise no major functional change.
// Our LZ77 compression engine
static void do_compress(BufferedWriter outfile, BufferedReader infile) throws Throwable {
// create queue (sliding window)
int window = 1024;
byte[] data = new byte[window];
int inptr = 0;
int outptr = 0;
int curptr = 0;
// simply copy at first
while (infile.ready()) {
// obtain next byte
int ch = infile.read();
// matching (cannot yet so just output byte)
outfile.write(ch);
curptr++;
if (curptr == window)
curptr = 0;
// queue uncompressed data
data[inptr++] = (byte)ch;
if (inptr == window)
inptr = 0;
if (inptr == outptr) {
outptr++;
if (outptr == window)
outptr = 0;
}
}
}
Now how are we going to do this “watching for matches” thing?
Let’s create the concept of an active match. At any given time we there will be from 0 to some number of active matches. Each will represent a match to the sequence of bytes appearing at the an input stream position. As new bytes are retrieved from the uncompressed input stream we will check any active matches and advance them . If a match is no longer valid it will be removed and forgotten. At that point though maybe the match warrants replacement in the stream with a pointer. We will see.
I made the data queue and related pointers static members of the program and created the following class representing an active match.
// An active match. At any given position in the sliding WINDOW we compare and track
// matches to the incoming DATA stream.
class match {
public int start;
public int ptr;
public int len;
match(int pos) {
start = pos;
ptr = pos + 1;
if (ptr == WINDOW)
ptr = 0;
len = 1;
}
public boolean check(int ch) {
if (DATA[ptr] != ch)
return (false);
ptr++;
if (ptr == WINDOW)
ptr = 0;
len++;
return (true);
}
}
When a new data byte is entered into the queue we will want to create these active match objects for every matching byte that previously exists. Every one of those represents a potential sequence.
Okay when we enter a new byte in the queue it becomes a candidate for replacement by a reference to a sequence starting with the byte somewhere earlier. So we want to start a new active match for the earlier bytes. We will process these matches as additional bytes are received from the input stream. To do this though we don’t want to search the entire window for prior existences of each character. So to make things efficient I am going to maintain linked lists through the queue for each character.
Since a byte can have 256 values we create a HEAD pointer array with 256 entries. This is referenced using the byte value. Each queue position then will have both a forward FWD and backwards BACK pointer forming a bi-directional linked list. Yeah, this quintuples our memory requirement but with the benefit of processing speed.
The list has to be bi-directional because once the queue fills we are going to drop bytes. It is then necessary to trim the linked lists to remove pointers for data no longer in the queue. That can only be done efficiently if we can reference a previous entry in the linked list. So we need both directions.
Here are our static members so far. This is the memory usage.
// create queue (sliding window)
static final int WINDOW = 1024;
static final byte[] DATA = new byte[WINDOW];
static int INPTR = 0;
static int OUTPTR = 0;
static int CURPTR = 0;
// data linked list arrays
static final short[] HEAD = new short[256];
static final short[] FWD = new short[WINDOW];
static final short[] BACK = new short[WINDOW];
Now we maintain the linked lists as we add and remove data from the queue. We also can efficiently create new active match objects. Note that we store pointers in the links as +1 so as to keep 0 as a terminator.
// queue uncompressed DATA
DATA[INPTR] = (byte)ch;
// Add byte to the head of the appropriate linked list. Note pointers are stored +1 so
// as to use 0 as an end of list marker. Lists are bi-directional so we can trim the
// tail when data is dropped from the queue.
short ptr = HEAD[ch];
HEAD[ch] = (short)(INPTR + 1);
FWD[INPTR] = ptr;
BACK[INPTR] = 0;
if (ptr != 0)
BACK[ptr - 1] = (short)(INPTR + 1);
// advance entry pointer
INPTR++;
if (INPTR == WINDOW)
INPTR = 0;
// drop data from queue when full
if (INPTR == OUTPTR) {
// trim linked list as byte is being dropped
if (BACK[OUTPTR] == 0)
HEAD[DATA[OUTPTR]] = 0;
else
FWD[BACK[OUTPTR] - 1] = 0;
// push end of queue
OUTPTR++;
if (OUTPTR == WINDOW)
OUTPTR = 0;
}
// create new active match for all CH in the queue (except last)
while (ptr != 0) {
// new match started (not doing anything with it yet)
match m = new match(ptr - 1);
ptr = FWD[ptr - 1];
}
I adjusted the program to dump non-zero HEAD entries and each occupied queue position including the links as a check. Remember that links are stored in here +1.
bruce_dev /> jtest blah.dat HEAD 0x0a 21 0x0d 20 0x20 15 0x42 1 0x61 18 0x62 16 0x68 19 0x6c 17 QUEUE 0 0x42 0 0 1 0x6c 0 7 2 0x61 0 8 3 0x68 0 9 4 0x20 0 10 5 0x62 0 11 6 0x6c 2 12 7 0x61 3 13 8 0x68 4 14 9 0x20 5 15 10 0x62 6 16 11 0x6c 7 17 12 0x61 8 18 13 0x68 9 19 14 0x20 10 0 15 0x62 11 0 16 0x6c 12 0 17 0x61 13 0 18 0x68 14 0 19 0x0d 0 0 20 0x0a 0 0 STATS Processing 0.078 seconds. Source 21 bytes. Result 21 bytes. Ratio 0.00% bruce_dev />
Now as we create new active matches we are going to collect them in an ArrayList object.
// active matching
static ArrayList SEQ = new ArrayList();
// create new active matches for all CH in the queue (except last)
while (ptr != 0) {
SEQ.add(new match(ptr - 1));
ptr = FWD[ptr - 1];
}
So as each new data byte is retrieved from the uncompressed input stream we will process all active matches. Those that continue to match will be retained and others dropped. That code looks like this:
// process uncompressed stream
while (infile.ready()) {
// obtain next byte
int ch = infile.read();
// process active match objects
System.out.printf("New byte[%d]: 0x%02x\n", INPTR, ch & 0xff);
for (int n = SEQ.size() - 1; 0 <= n; n--) {
match m = SEQ.get(n);
if (!m.check(ch))
SEQ.remove(n);
}
If following this if I dump the remaining active matches we can watch those proceed. At this point though we have not interpreted the matching status so as to decide whether or not the stream can be altered.
// dump remaining active matches
Iterator i = SEQ.iterator();
while (i.hasNext()) {
match m = (match) i.next();
System.out.printf(" Start: %d Ptr: %d Len: %d\n", m.start, m.ptr, m.len);
}
So in reviewing the An Explanation of the DEFLATE Algorithm paper from 1997:
Antaeus Feldspar wrote:LZ77 compression
LZ77 compression works by finding sequences of data that are repeated. The term “sliding window” is used; all it really means is that at any given point in the data, there is a record of what characters went before. A 32K sliding window means that the compressor (and decompressor) have a record of what the last 32768 (32 * 1024) characters were. When the next sequence of characters to be compressed is identical to one that can be found within the sliding window, the sequence of characters is replaced by two numbers: a distance, representing how far back into the window the sequence starts, and a length, representing the number of characters for which the sequence is identical.
I realize this is a lot easier to see than to just be told. Let’s look at some highly compressible data:
Blah blah blah blah blah!Our datastream starts by receiving the following characters: “B,” “l,” “a,” “h,” ” ,” and “b.” However, look at the next five characters:
vvvvv Blah blah blah blah blah! ^^^^^There is an exact match for those five characters in the characters that have already gone into the datastream, and it starts exactly five characters behind the point where we are now. This being the case, we can output special characters to the stream that represent a number for length, and a number for distance.
The data so far:
Blah blah bThe compressed form of the data so far:
Blah b[D=5,L=5]The compression can still be increased, though to take full advantage of it requires a bit of cleverness on the part of the compressor. Look at the two strings that we decided were identical. Compare the character that follows each of them. In both cases, it’s “l” — so we can make the length 6, and not just five. But if we continue checking, we find the next characters, and the next characters, and the next characters, are still identical — even if the so-called ‘previous’ string is overlapping the string we’re trying to represent in the compressed data!
It turns out that the 18 characters that start at the second character are identical to the 18 characters that start at the seventh character. It’s true that when we’re decompressing, and read the length, distance pair that describes this relationship, we don’t know what all those 18 characters will be yet — but if we put in place the ones that we know, we will know more, which will allow us to put down more… or, knowing that any length-and-distance pair where length > distance is going to be repeating (distance) characters again and again, we can set up the decompressor to do just that.
It turns out our highly compressible data can be compressed down to just this:
Blah b[D=5, L=18]!
So if I feed this exact stream to what we have so far we can observe the sequencing:
bruce_dev /> echo Blah blah blah blah blah! > blah.dat
bruce_dev /> cat blah.dat
Blah blah blah blah blah!
bruce_dev /> jtest blah.dat
New byte[0]: 0x42
New byte[1]: 0x6c
New byte[2]: 0x61
New byte[3]: 0x68
New byte[4]: 0x20
New byte[5]: 0x62
New byte[6]: 0x6c
New byte[7]: 0x61
Start: 1 Ptr: 3 Len: 2
New byte[8]: 0x68
Start: 1 Ptr: 4 Len: 3
Start: 2 Ptr: 4 Len: 2
New byte[9]: 0x20
Start: 1 Ptr: 5 Len: 4
Start: 2 Ptr: 5 Len: 3
Start: 3 Ptr: 5 Len: 2
New byte[10]: 0x62
Start: 1 Ptr: 6 Len: 5
Start: 2 Ptr: 6 Len: 4
Start: 3 Ptr: 6 Len: 3
Start: 4 Ptr: 6 Len: 2
New byte[11]: 0x6c
Start: 1 Ptr: 7 Len: 6
Start: 2 Ptr: 7 Len: 5
Start: 3 Ptr: 7 Len: 4
Start: 4 Ptr: 7 Len: 3
Start: 5 Ptr: 7 Len: 2
New byte[12]: 0x61
Start: 1 Ptr: 8 Len: 7
Start: 2 Ptr: 8 Len: 6
Start: 3 Ptr: 8 Len: 5
Start: 4 Ptr: 8 Len: 4
Start: 5 Ptr: 8 Len: 3
Start: 6 Ptr: 8 Len: 2
Start: 1 Ptr: 3 Len: 2
New byte[13]: 0x68
Start: 1 Ptr: 9 Len: 8
Start: 2 Ptr: 9 Len: 7
Start: 3 Ptr: 9 Len: 6
Start: 4 Ptr: 9 Len: 5
Start: 5 Ptr: 9 Len: 4
Start: 6 Ptr: 9 Len: 3
Start: 1 Ptr: 4 Len: 3
Start: 7 Ptr: 9 Len: 2
Start: 2 Ptr: 4 Len: 2
New byte[14]: 0x20
Start: 1 Ptr: 10 Len: 9
Start: 2 Ptr: 10 Len: 8
Start: 3 Ptr: 10 Len: 7
Start: 4 Ptr: 10 Len: 6
Start: 5 Ptr: 10 Len: 5
Start: 6 Ptr: 10 Len: 4
Start: 1 Ptr: 5 Len: 4
Start: 7 Ptr: 10 Len: 3
Start: 2 Ptr: 5 Len: 3
Start: 8 Ptr: 10 Len: 2
Start: 3 Ptr: 5 Len: 2
New byte[15]: 0x62
Start: 1 Ptr: 11 Len: 10
Start: 2 Ptr: 11 Len: 9
Start: 3 Ptr: 11 Len: 8
Start: 4 Ptr: 11 Len: 7
Start: 5 Ptr: 11 Len: 6
Start: 6 Ptr: 11 Len: 5
Start: 1 Ptr: 6 Len: 5
Start: 7 Ptr: 11 Len: 4
Start: 2 Ptr: 6 Len: 4
Start: 8 Ptr: 11 Len: 3
Start: 3 Ptr: 6 Len: 3
Start: 9 Ptr: 11 Len: 2
Start: 4 Ptr: 6 Len: 2
New byte[16]: 0x6c
Start: 1 Ptr: 12 Len: 11
Start: 2 Ptr: 12 Len: 10
Start: 3 Ptr: 12 Len: 9
Start: 4 Ptr: 12 Len: 8
Start: 5 Ptr: 12 Len: 7
Start: 6 Ptr: 12 Len: 6
Start: 1 Ptr: 7 Len: 6
Start: 7 Ptr: 12 Len: 5
Start: 2 Ptr: 7 Len: 5
Start: 8 Ptr: 12 Len: 4
Start: 3 Ptr: 7 Len: 4
Start: 9 Ptr: 12 Len: 3
Start: 4 Ptr: 7 Len: 3
Start: 10 Ptr: 12 Len: 2
Start: 5 Ptr: 7 Len: 2
New byte[17]: 0x61
Start: 1 Ptr: 13 Len: 12
Start: 2 Ptr: 13 Len: 11
Start: 3 Ptr: 13 Len: 10
Start: 4 Ptr: 13 Len: 9
Start: 5 Ptr: 13 Len: 8
Start: 6 Ptr: 13 Len: 7
Start: 1 Ptr: 8 Len: 7
Start: 7 Ptr: 13 Len: 6
Start: 2 Ptr: 8 Len: 6
Start: 8 Ptr: 13 Len: 5
Start: 3 Ptr: 8 Len: 5
Start: 9 Ptr: 13 Len: 4
Start: 4 Ptr: 8 Len: 4
Start: 10 Ptr: 13 Len: 3
Start: 5 Ptr: 8 Len: 3
Start: 11 Ptr: 13 Len: 2
Start: 6 Ptr: 8 Len: 2
Start: 1 Ptr: 3 Len: 2
New byte[18]: 0x68
Start: 1 Ptr: 14 Len: 13
Start: 2 Ptr: 14 Len: 12
Start: 3 Ptr: 14 Len: 11
Start: 4 Ptr: 14 Len: 10
Start: 5 Ptr: 14 Len: 9
Start: 6 Ptr: 14 Len: 8
Start: 1 Ptr: 9 Len: 8
Start: 7 Ptr: 14 Len: 7
Start: 2 Ptr: 9 Len: 7
Start: 8 Ptr: 14 Len: 6
Start: 3 Ptr: 9 Len: 6
Start: 9 Ptr: 14 Len: 5
Start: 4 Ptr: 9 Len: 5
Start: 10 Ptr: 14 Len: 4
Start: 5 Ptr: 9 Len: 4
Start: 11 Ptr: 14 Len: 3
Start: 6 Ptr: 9 Len: 3
Start: 1 Ptr: 4 Len: 3
Start: 12 Ptr: 14 Len: 2
Start: 7 Ptr: 9 Len: 2
Start: 2 Ptr: 4 Len: 2
New byte[19]: 0x20
Start: 1 Ptr: 15 Len: 14
Start: 2 Ptr: 15 Len: 13
Start: 3 Ptr: 15 Len: 12
Start: 4 Ptr: 15 Len: 11
Start: 5 Ptr: 15 Len: 10
Start: 6 Ptr: 15 Len: 9
Start: 1 Ptr: 10 Len: 9
Start: 7 Ptr: 15 Len: 8
Start: 2 Ptr: 10 Len: 8
Start: 8 Ptr: 15 Len: 7
Start: 3 Ptr: 10 Len: 7
Start: 9 Ptr: 15 Len: 6
Start: 4 Ptr: 10 Len: 6
Start: 10 Ptr: 15 Len: 5
Start: 5 Ptr: 10 Len: 5
Start: 11 Ptr: 15 Len: 4
Start: 6 Ptr: 10 Len: 4
Start: 1 Ptr: 5 Len: 4
Start: 12 Ptr: 15 Len: 3
Start: 7 Ptr: 10 Len: 3
Start: 2 Ptr: 5 Len: 3
Start: 13 Ptr: 15 Len: 2
Start: 8 Ptr: 10 Len: 2
Start: 3 Ptr: 5 Len: 2
New byte[20]: 0x62
Start: 1 Ptr: 16 Len: 15
Start: 2 Ptr: 16 Len: 14
Start: 3 Ptr: 16 Len: 13
Start: 4 Ptr: 16 Len: 12
Start: 5 Ptr: 16 Len: 11
Start: 6 Ptr: 16 Len: 10
Start: 1 Ptr: 11 Len: 10
Start: 7 Ptr: 16 Len: 9
Start: 2 Ptr: 11 Len: 9
Start: 8 Ptr: 16 Len: 8
Start: 3 Ptr: 11 Len: 8
Start: 9 Ptr: 16 Len: 7
Start: 4 Ptr: 11 Len: 7
Start: 10 Ptr: 16 Len: 6
Start: 5 Ptr: 11 Len: 6
Start: 11 Ptr: 16 Len: 5
Start: 6 Ptr: 11 Len: 5
Start: 1 Ptr: 6 Len: 5
Start: 12 Ptr: 16 Len: 4
Start: 7 Ptr: 11 Len: 4
Start: 2 Ptr: 6 Len: 4
Start: 13 Ptr: 16 Len: 3
Start: 8 Ptr: 11 Len: 3
Start: 3 Ptr: 6 Len: 3
Start: 14 Ptr: 16 Len: 2
Start: 9 Ptr: 11 Len: 2
Start: 4 Ptr: 6 Len: 2
New byte[21]: 0x6c
Start: 1 Ptr: 17 Len: 16
Start: 2 Ptr: 17 Len: 15
Start: 3 Ptr: 17 Len: 14
Start: 4 Ptr: 17 Len: 13
Start: 5 Ptr: 17 Len: 12
Start: 6 Ptr: 17 Len: 11
Start: 1 Ptr: 12 Len: 11
Start: 7 Ptr: 17 Len: 10
Start: 2 Ptr: 12 Len: 10
Start: 8 Ptr: 17 Len: 9
Start: 3 Ptr: 12 Len: 9
Start: 9 Ptr: 17 Len: 8
Start: 4 Ptr: 12 Len: 8
Start: 10 Ptr: 17 Len: 7
Start: 5 Ptr: 12 Len: 7
Start: 11 Ptr: 17 Len: 6
Start: 6 Ptr: 12 Len: 6
Start: 1 Ptr: 7 Len: 6
Start: 12 Ptr: 17 Len: 5
Start: 7 Ptr: 12 Len: 5
Start: 2 Ptr: 7 Len: 5
Start: 13 Ptr: 17 Len: 4
Start: 8 Ptr: 12 Len: 4
Start: 3 Ptr: 7 Len: 4
Start: 14 Ptr: 17 Len: 3
Start: 9 Ptr: 12 Len: 3
Start: 4 Ptr: 7 Len: 3
Start: 15 Ptr: 17 Len: 2
Start: 10 Ptr: 12 Len: 2
Start: 5 Ptr: 7 Len: 2
New byte[22]: 0x61
Start: 1 Ptr: 18 Len: 17
Start: 2 Ptr: 18 Len: 16
Start: 3 Ptr: 18 Len: 15
Start: 4 Ptr: 18 Len: 14
Start: 5 Ptr: 18 Len: 13
Start: 6 Ptr: 18 Len: 12
Start: 1 Ptr: 13 Len: 12
Start: 7 Ptr: 18 Len: 11
Start: 2 Ptr: 13 Len: 11
Start: 8 Ptr: 18 Len: 10
Start: 3 Ptr: 13 Len: 10
Start: 9 Ptr: 18 Len: 9
Start: 4 Ptr: 13 Len: 9
Start: 10 Ptr: 18 Len: 8
Start: 5 Ptr: 13 Len: 8
Start: 11 Ptr: 18 Len: 7
Start: 6 Ptr: 13 Len: 7
Start: 1 Ptr: 8 Len: 7
Start: 12 Ptr: 18 Len: 6
Start: 7 Ptr: 13 Len: 6
Start: 2 Ptr: 8 Len: 6
Start: 13 Ptr: 18 Len: 5
Start: 8 Ptr: 13 Len: 5
Start: 3 Ptr: 8 Len: 5
Start: 14 Ptr: 18 Len: 4
Start: 9 Ptr: 13 Len: 4
Start: 4 Ptr: 8 Len: 4
Start: 15 Ptr: 18 Len: 3
Start: 10 Ptr: 13 Len: 3
Start: 5 Ptr: 8 Len: 3
Start: 16 Ptr: 18 Len: 2
Start: 11 Ptr: 13 Len: 2
Start: 6 Ptr: 8 Len: 2
Start: 1 Ptr: 3 Len: 2
New byte[23]: 0x68
Start: 1 Ptr: 19 Len: 18
Start: 2 Ptr: 19 Len: 17
Start: 3 Ptr: 19 Len: 16
Start: 4 Ptr: 19 Len: 15
Start: 5 Ptr: 19 Len: 14
Start: 6 Ptr: 19 Len: 13
Start: 1 Ptr: 14 Len: 13
Start: 7 Ptr: 19 Len: 12
Start: 2 Ptr: 14 Len: 12
Start: 8 Ptr: 19 Len: 11
Start: 3 Ptr: 14 Len: 11
Start: 9 Ptr: 19 Len: 10
Start: 4 Ptr: 14 Len: 10
Start: 10 Ptr: 19 Len: 9
Start: 5 Ptr: 14 Len: 9
Start: 11 Ptr: 19 Len: 8
Start: 6 Ptr: 14 Len: 8
Start: 1 Ptr: 9 Len: 8
Start: 12 Ptr: 19 Len: 7
Start: 7 Ptr: 14 Len: 7
Start: 2 Ptr: 9 Len: 7
Start: 13 Ptr: 19 Len: 6
Start: 8 Ptr: 14 Len: 6
Start: 3 Ptr: 9 Len: 6
Start: 14 Ptr: 19 Len: 5
Start: 9 Ptr: 14 Len: 5
Start: 4 Ptr: 9 Len: 5
Start: 15 Ptr: 19 Len: 4
Start: 10 Ptr: 14 Len: 4
Start: 5 Ptr: 9 Len: 4
Start: 16 Ptr: 19 Len: 3
Start: 11 Ptr: 14 Len: 3
Start: 6 Ptr: 9 Len: 3
Start: 1 Ptr: 4 Len: 3
Start: 17 Ptr: 19 Len: 2
Start: 12 Ptr: 14 Len: 2
Start: 7 Ptr: 9 Len: 2
Start: 2 Ptr: 4 Len: 2
New byte[24]: 0x21
New byte[25]: 0x0d
New byte[26]: 0x0a
Processing 2.494 seconds.
Source 27 bytes.
Result 27 bytes.
Ratio 0.00%
bruce_dev /> Now the ‘D’ in the paper refers to the distance between our CURPTR at the point when a match is started and the matched sequence position. If you persevere through the above you can verify that D=5 would be correct and that our best match ran through the length of 18.
So we now need the logic controlling the advancement of CURPTR and what then to output to the compressed stream.
So the strategy at this point is to process all active matches. We don’t move the CURPTR when there is at least one potential match still in the works. When a data byte is received that does not extend a match we remove that match from the array. We keep track of the best of the matches that terminate as that would be a candidate for using a reference pointer if none remain active.
// Our LZ77 compression engine
static void do_compress(BufferedWriter outfile, BufferedReader infile) throws Throwable {
// process uncompressed stream
while (infile.ready()) {
// obtain next byte
int ch = infile.read();
System.out.print((char)ch);
// process active match objects
boolean bActive = false;
match best = null;
for (int n = SEQ.size() - 1; 0 <= n; n--) { match m = SEQ.get(n); if (!m.check(ch)) { if (m.curptr == CURPTR && best == null && m.len >= 3)
best = m;
SEQ.remove(n);
}
else if (m.curptr == CURPTR)
bActive = true;
}
From the above bActive will be true if there remain potentially longer sequences. In that case we will not do anything with CURPTR or output anything. We just eventually move on to process the next byte from the uncompressed input stream.
If bActive is false and best remains null then the byte at CURPTR will be output and CURPTR advanced.
Otherwise we have match to something in the sliding window and that can replace the uncompressed sequence.
// If there is no active sequence then we need to generate some output
if (!bActive) {
// If there's been no match then we output data as is
if (best == null) {
while (CURPTR != INPTR) {
outfile.write(DATA[CURPTR]);
CURPTR++;
if (CURPTR == WINDOW)
CURPTR = 0;
int n;
for (n = SEQ.size() - 1; 0 <= n; n--) {
match m = SEQ.get(n);
if (m.curptr == CURPTR)
break;
}
if (0 <= n)
break;
}
}
// otherwise we can substitute
else {
int distance = best.curptr - best.start;
if (distance < 0) distance += WINDOW; String msg = String.format("[D=%d, L=%d]", distance, best.len); outfile.write(msg); // flush active matches int len = best.len; while (len-- > 0) {
CURPTR++;
if (CURPTR == WINDOW)
CURPTR = 0;
// remove overlapped active sequences
for (int n = SEQ.size() - 1; 0 <= n; n--) {
match m = SEQ.get(n);
if (m.curptr == CURPTR)
SEQ.remove(n);
}
}
}
}
In the above when we are outputting data uncompressed from CURPTR we continue until we encounter an active match. When we replace a sequence we flush any active matches involving the data replaced. Those matches (which potentially could be more beneficial) are no longer valid. Note that for debugging I am outputting the [D= L=] format so I can see what is being replaced and how more clearly.
Later the best match would also be the one with the lowest distance. That saves bits and takes advantage of the Huffman Coding which we have yet to implement.
The output using the above logic and debugging looks like this for the blah blah test data.
bruce_dev /> jtest blah.dat Blah blah blah blah blah! Processing 0.856 seconds. Source 27 bytes. Result 19 bytes. Ratio 29.63% bruce_dev /> cat outfile.dat Blah b[D=5, L=18]! bruce_dev />
This agrees nicely with the example from the paper. This works with more elaborate data as well. I know that this is a Java prototype but it seems even a bit too slow for larger files even considering the platform. I get the feeling that I am creating far too many new active match objects. Perhaps there is some logic as to what is worth creating and what isn’t.
It turns out that I am likely creating 3X the number of active match objects than is necessary however the overhead to detect them slows the process way too much. It seems better to create the unnecessary match objects and optimize them out later.
I decided to take a step back and not try to generate the compressed output stream just yet. Instead I want to look at the sequence matches that I detect to see what logic I would need to achieve an optimal compression. There is this lazy match optimization to consider.
You might recall that the approach is that when I retrieve a byte from the uncompressed input stream I process all of the active sequence match objects. If the new character extends a match then it remains active. Otherwise the sequence is complete and we decide whether it is useful or not before removing it from the active match list. A useful match is simply one that is 3 or more bytes in length.
The uncompressed data byte is queued (enters the sliding window) and we create new active sequence matches for every matching bat still in the window. We use a linked list to efficiently locate those characters.
If we simply list those potentially useful matches the code looks like what follows.
// Our LZ77 compression engine
static void do_compress(BufferedWriter outfile, BufferedReader infile) throws Throwable {
// process uncompressed stream
while (infile.ready()) {
// obtain next byte
int ch = infile.read();
//System.out.print((char)ch);
// process active Match objects
for (int n = SEQ.size() - 1; 0 <= n; n--) { Match m = SEQ.get(n); if (!m.check(ch)) { if (m.len >= 3) {
System.out.printf("I=%04x C=%04x P=%04x, D=%d, L=%d\n",
INPTR, m.curptr, m.start, m.distance, m.len);
}
SEQ.remove(n);
}
}
// queue uncompressed DATA
int inp = INPTR;
DATA[INPTR] = (byte)ch;
// Add byte to the head of the appropriate linked list. Note pointers are stored +1 so
// as to use 0 as an end of list marker. Lists are bi-directional so we can trim the
// tail when data is dropped from the queue.
short ptr = HEAD[ch];
HEAD[ch] = (short)(INPTR + 1);
FWD[INPTR] = ptr;
BACK[INPTR] = 0;
if (ptr != 0)
BACK[ptr - 1] = (short)(INPTR + 1);
// advance entry pointer
INPTR++;
if (INPTR == WINDOW)
INPTR = 0;
// drop data from queue when full
if (INPTR == OUTPTR) {
// trim linked list as byte is being dropped
if (BACK[OUTPTR] == 0)
HEAD[DATA[OUTPTR]] = 0;
else
FWD[BACK[OUTPTR] - 1] = 0;
// push end of queue
OUTPTR++;
if (OUTPTR == WINDOW)
OUTPTR = 0;
}
// create new active matches for all CH in the queue (except last)
while (ptr != 0) {
SEQ.add(new Match(inp, ptr - 1));
ptr = FWD[ptr - 1];
}
}
}
Now we display the match results with pointers in hex so we can locate them in a hex dump. These are ‘I’ giving the uncompressed input position; ‘C’ showing the input position when the match was created; ‘P’ is the position in the sliding window or queue; ‘D’ is the distance (basically C minus P); And, ‘L’ the length of the match. We get the following for the blah blah data.
bruce_dev /> cat blah.dat -h
00000000 42 6c 61 68 20 62 6c 61 68 20 62 6c 61 68 20 62 Blah.bla h.blah.b
00000010 6c 61 68 20 62 6c 61 68 21 0d 0a lah.blah !..
bruce_dev /> jtest blah.dat
I=0018 C=0015 P=0001, D=20, L=3
I=0018 C=0015 P=0006, D=15, L=3
I=0018 C=0015 P=000b, D=10, L=3
I=0018 C=0015 P=0010, D=5, L=3
I=0018 C=0014 P=0005, D=15, L=4
I=0018 C=0014 P=000a, D=10, L=4
I=0018 C=0014 P=000f, D=5, L=4
I=0018 C=0013 P=0004, D=15, L=5
I=0018 C=0013 P=0009, D=10, L=5
I=0018 C=0013 P=000e, D=5, L=5
I=0018 C=0012 P=0003, D=15, L=6
I=0018 C=0012 P=0008, D=10, L=6
I=0018 C=0012 P=000d, D=5, L=6
I=0018 C=0011 P=0002, D=15, L=7
I=0018 C=0011 P=0007, D=10, L=7
I=0018 C=0011 P=000c, D=5, L=7
I=0018 C=0010 P=0001, D=15, L=8
I=0018 C=0010 P=0006, D=10, L=8
I=0018 C=0010 P=000b, D=5, L=8
I=0018 C=000f P=0005, D=10, L=9
I=0018 C=000f P=000a, D=5, L=9
I=0018 C=000e P=0004, D=10, L=10
I=0018 C=000e P=0009, D=5, L=10
I=0018 C=000d P=0003, D=10, L=11
I=0018 C=000d P=0008, D=5, L=11
I=0018 C=000c P=0002, D=10, L=12
I=0018 C=000c P=0007, D=5, L=12
I=0018 C=000b P=0001, D=10, L=13
I=0018 C=000b P=0006, D=5, L=13
I=0018 C=000a P=0005, D=5, L=14
I=0018 C=0009 P=0004, D=5, L=15
I=0018 C=0008 P=0003, D=5, L=16
I=0018 C=0007 P=0002, D=5, L=17
I=0018 C=0006 P=0001, D=5, L=18
Processing 1.063 seconds.
Source 27 bytes.
Result 0 bytes.
Ratio 100.00%
bruce_dev />You can see from this that we are processing a lot of matches for what we know will be just one replacement. You can see that for each new byte received (at C) we create potential matches for all matching bytes (1 or more P) each with a fixed D. We then have advanced the length L as additional characters extend the match.
Of all these matches completed there will be one best match. That would be the longest match (largest L) and if there is a choice between multiple matches of the same length (L) we would take the one with lowest distance (D).
Now let me add logic to select the best match and only display that one. I am also going to display a marker (“—-“) when we reach a point in the input stream after having found at least one match when there are no active matches in process. That point would be a good time to generate the compressed data based on the matching sequences we’ve found.
So that section of the code now looks like this.
// Our LZ77 compression engine
static void do_compress(BufferedWriter outfile, BufferedReader infile) throws Throwable {
boolean bFound = false;
// process uncompressed stream
while (infile.ready()) {
// obtain next byte
int ch = infile.read();
//System.out.print((char)ch);
// process active Match objects
Match best = null;
for (int n = SEQ.size() - 1; 0 <= n; n--) { Match m = SEQ.get(n); if (!m.check(ch)) { if (m.len >= 3) {
if (best == null)
best = m;
else if (m.len > best.len)
best = m;
else if (m.len == best.len && m.distance < best.distance)
best = m;
}
SEQ.remove(n);
}
}
if (best != null) {
System.out.printf("I=%04x C=%04x P=%04x, D=%d, L=%d\n",
INPTR, best.curptr, best.start, best.distance, best.len);
bFound = true;
}
if (bFound && SEQ.size() == 0) {
System.out.println("----");
bFound = false;
}
// queue uncompressed DATA
Processing the blah blah data yield the following which we have seen is the replacement that we are hoping for.
bruce_dev /> cat blah.dat -h
00000000 42 6c 61 68 20 62 6c 61 68 20 62 6c 61 68 20 62 Blah.bla h.blah.b
00000010 6c 61 68 20 62 6c 61 68 21 0d 0a lah.blah !..
bruce_dev /> jtest blah.dat
I=0018 C=0006 P=0001, D=5, L=18
----
Processing 0.819 seconds.
Source 27 bytes.
Result 0 bytes.
Ratio 100.00%
bruce_dev /> What about some more involved input data?
bruce_dev /> cat jniorboot.log -h
00000000 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 01/04/18 .08:19:1
00000010 38 2e 31 31 31 2c 20 2a 2a 20 4f 53 20 43 52 43 8.111,.* *.OS.CRC
00000020 20 64 65 74 61 69 6c 20 75 70 64 61 74 65 64 0d .detail. updated.
00000030 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a .01/04/1 8.08:19:
00000040 31 38 2e 31 35 38 2c 20 2d 2d 20 4d 6f 64 65 6c 18.158,. --.Model
00000050 20 34 31 30 20 76 31 2e 36 2e 33 20 2d 20 4a 41 .410.v1. 6.3.-.JA
00000060 4e 4f 53 20 53 65 72 69 65 73 20 34 0d 0a 30 31 NOS.Seri es.4..01
00000070 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e /04/18.0 8:19:18.
00000080 31 37 38 2c 20 43 6f 70 79 72 69 67 68 74 20 28 178,.Cop yright.(
00000090 63 29 20 32 30 31 32 2d 32 30 31 38 20 49 4e 54 c).2012- 2018.INT
000000A0 45 47 20 50 72 6f 63 65 73 73 20 47 72 6f 75 70 EG.Proce ss.Group
000000B0 2c 20 49 6e 63 2e 2c 20 47 69 62 73 6f 6e 69 61 ,.Inc.,. Gibsonia
000000C0 20 50 41 20 55 53 41 0d 0a 30 31 2f 30 34 2f 31 .PA.USA. .01/04/1
000000D0 38 20 30 38 3a 31 39 3a 31 38 2e 31 39 37 2c 20 8.08:19: 18.197,.
000000E0 4a 41 4e 4f 53 20 77 72 69 74 74 65 6e 20 61 6e JANOS.wr itten.an
000000F0 64 20 64 65 76 65 6c 6f 70 65 64 20 62 79 20 42 d.develo ped.by.B
00000100 72 75 63 65 20 43 6c 6f 75 74 69 65 72 0d 0a 30 ruce.Clo utier..0
00000110 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 1/04/18. 08:19:18
00000120 2e 32 31 36 2c 20 53 65 72 69 61 6c 20 4e 75 6d .216,.Se rial.Num
00000130 62 65 72 3a 20 36 31 34 30 37 30 35 30 30 0d 0a ber:.614 070500..
00000140 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 01/04/18 .08:19:1
00000150 38 2e 32 33 36 2c 20 46 69 6c 65 20 53 79 73 74 8.236,.F ile.Syst
00000160 65 6d 20 6d 6f 75 6e 74 65 64 0d 0a 30 31 2f 30 em.mount ed..01/0
00000170 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e 32 35 4/18.08: 19:18.25
00000180 37 2c 20 52 65 67 69 73 74 72 79 20 6d 6f 75 6e 7,.Regis try.moun
00000190 74 65 64 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 ted..01/ 04/18.08
000001A0 3a 31 39 3a 31 38 2e 33 30 36 2c 20 4e 65 74 77 :19:18.3 06,.Netw
000001B0 6f 72 6b 20 49 6e 69 74 69 61 6c 69 7a 65 64 0d ork.Init ialized.
000001C0 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a .01/04/1 8.08:19:
000001D0 31 38 2e 33 32 36 2c 20 45 74 68 65 72 6e 65 74 18.326,. Ethernet
000001E0 20 41 64 64 72 65 73 73 3a 20 39 63 3a 38 64 3a .Address :.9c:8d:
000001F0 31 61 3a 30 30 3a 30 37 3a 65 65 0d 0a 30 31 2f 1a:00:07 :ee..01/
00000200 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e 34 04/18.08 :19:18.4
00000210 34 37 2c 20 53 65 6e 73 6f 72 20 50 6f 72 74 20 47,.Sens or.Port.
00000220 69 6e 69 74 69 61 6c 69 7a 65 64 0d 0a 30 31 2f initiali zed..01/
00000230 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e 35 04/18.08 :19:18.5
00000240 30 32 2c 20 49 2f 4f 20 73 65 72 76 69 63 65 73 02,.I/O. services
00000250 20 69 6e 69 74 69 61 6c 69 7a 65 64 0d 0a 30 31 .initial ized..01
00000260 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e /04/18.0 8:19:18.
00000270 35 33 35 2c 20 46 54 50 20 73 65 72 76 65 72 20 535,.FTP .server.
00000280 65 6e 61 62 6c 65 64 20 66 6f 72 20 70 6f 72 74 enabled. for.port
00000290 20 32 31 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 .21..01/ 04/18.08
000002A0 3a 31 39 3a 31 38 2e 35 35 36 2c 20 50 72 6f 74 :19:18.5 56,.Prot
000002B0 6f 63 6f 6c 20 73 65 72 76 65 72 20 65 6e 61 62 ocol.ser ver.enab
000002C0 6c 65 64 20 66 6f 72 20 70 6f 72 74 20 39 32 30 led.for. port.920
000002D0 30 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 0..01/04 /18.08:1
000002E0 39 3a 31 38 2e 35 38 36 2c 20 57 65 62 53 65 72 9:18.586 ,.WebSer
000002F0 76 65 72 20 65 6e 61 62 6c 65 64 20 66 6f 72 20 ver.enab led.for.
00000300 70 6f 72 74 20 38 30 0d 0a 30 31 2f 30 34 2f 31 port.80. .01/04/1
00000310 38 20 30 38 3a 31 39 3a 31 38 2e 36 30 38 2c 20 8.08:19: 18.608,.
00000320 54 65 6c 6e 65 74 20 73 65 72 76 65 72 20 65 6e Telnet.s erver.en
00000330 61 62 6c 65 64 20 66 6f 72 20 70 6f 72 74 20 32 abled.fo r.port.2
00000340 33 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 3..01/04 /18.08:1
00000350 39 3a 31 38 2e 36 33 32 2c 20 50 4f 52 3a 20 35 9:18.632 ,.POR:.5
00000360 39 32 36 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 926..01/ 04/18.08
00000370 3a 31 39 3a 31 38 2e 36 35 33 2c 20 43 75 6d 75 :19:18.6 53,.Cumu
00000380 6c 61 74 69 76 65 20 52 75 6e 74 69 6d 65 3a 20 lative.R untime:.
00000390 38 20 57 65 65 6b 73 20 35 20 44 61 79 73 20 31 8.Weeks. 5.Days.1
000003A0 20 48 6f 75 72 20 32 34 3a 33 32 2e 32 38 31 0d .Hour.24 :32.281.
000003B0 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a .01/04/1 8.08:19:
000003C0 31 38 2e 36 37 38 2c 20 42 6f 6f 74 20 43 6f 6d 18.678,. Boot.Com
000003D0 70 6c 65 74 65 64 20 5b 32 2e 33 20 73 65 63 6f pleted.[ 2.3.seco
000003E0 6e 64 73 5d 0d 0a nds]..
bruce_dev /> jtest jniorboot.log
I=0044 C=0031 P=0000, D=49, L=19
----
I=0064 C=0061 P=001a, D=71, L=3
----
I=0081 C=006c P=002f, D=61, L=21
----
I=0085 C=0082 P=0045, D=61, L=3
----
I=009b C=0098 P=0093, D=5, L=3
I=009d C=009a P=0074, D=38, L=3
----
I=00d2 C=00cf P=009a, D=53, L=3
I=00dc C=00c7 P=006c, D=91, L=21
----
I=00e6 C=00df P=005d, D=130, L=7
----
I=00f4 C=00f1 P=0020, D=209, L=3
----
I=0118 C=0115 P=009a, D=123, L=3
I=0121 C=010d P=00c7, D=70, L=20
----
I=012a C=0125 P=0063, D=194, L=5
----
I=0149 C=0146 P=009a, D=172, L=3
I=0152 C=013e P=00c7, D=119, L=20
I=0153 C=013e P=010d, D=49, L=21
----
I=0157 C=0154 P=0123, D=49, L=3
----
I=0175 C=0172 P=009a, D=216, L=3
I=017e C=0167 P=002c, D=315, L=23
I=017f C=016a P=013e, D=44, L=21
----
I=0183 C=0180 P=00dd, D=163, L=3
----
I=019e C=019b P=009a, D=257, L=3
I=01a7 C=018b P=0162, D=41, L=28
----
I=01ac C=01a9 P=0154, D=85, L=3
----
I=01b6 C=01b3 P=00b1, D=258, L=3
I=01bb C=01b8 P=0129, D=143, L=3
----
I=01ca C=01c7 P=009a, D=301, L=3
I=01d3 C=01bd P=0168, D=85, L=22
I=01d4 C=01bd P=0191, D=44, L=23
----
I=01d8 C=01d5 P=01a9, D=44, L=3
----
I=01e8 C=01e5 P=00a7, D=318, L=3
----
I=0206 C=0203 P=009a, D=361, L=3
I=020f C=01fb P=01bf, D=60, L=20
----
I=0214 C=0211 P=0180, D=145, L=3
I=0216 C=0212 P=0124, D=238, L=4
----
I=0227 C=0224 P=0129, D=251, L=3
I=0236 C=0233 P=009a, D=409, L=3
I=023f C=0221 P=01b5, D=108, L=30
----
I=0245 C=0242 P=00b0, D=402, L=3
----
I=0250 C=024d P=00a6, D=423, L=3
I=0251 C=024e P=0068, D=486, L=3
I=0258 C=0255 P=0129, D=300, L=3
I=0267 C=0264 P=009a, D=458, L=3
I=0270 C=0252 P=01b5, D=157, L=30
I=0271 C=0250 P=021f, D=49, L=33
----
I=0276 C=0273 P=0155, D=286, L=3
----
I=027d C=0278 P=0247, D=49, L=5
----
I=0288 C=0285 P=00f9, D=396, L=3
----
I=028c C=0289 P=0218, D=113, L=3
----
I=0291 C=028d P=021c, D=113, L=4
----
I=029e C=029b P=009a, D=513, L=3
I=02a7 C=0293 P=01fb, D=152, L=20
I=02a8 C=0293 P=025c, D=55, L=21
----
I=02ac C=02a9 P=01d5, D=212, L=3
I=02af C=02ab P=00a2, D=521, L=4
----
I=02b9 C=02b4 P=0247, D=109, L=5
I=02c4 C=02c1 P=00f9, D=456, L=3
I=02c8 C=02c5 P=0218, D=173, L=3
I=02cd C=02b4 P=0278, D=60, L=25
----
I=02dc C=02d9 P=009a, D=575, L=3
I=02e5 C=02cf P=013c, D=403, L=22
I=02e6 C=02d1 P=0293, D=62, L=21
----
I=02ea C=02e7 P=02a9, D=62, L=3
----
I=02f0 C=02ed P=0126, D=455, L=3
I=02f1 C=02ee P=0249, D=165, L=3
I=02fc C=02f9 P=00f9, D=512, L=3
I=0300 C=02fd P=0218, D=229, L=3
I=0305 C=02ee P=02b6, D=56, L=23
----
I=0312 C=030f P=009a, D=629, L=3
I=031b C=0306 P=02d0, D=54, L=21
----
I=0320 C=031d P=0082, D=667, L=3
----
I=0327 C=0323 P=01dd, D=326, L=4
I=032b C=0326 P=0247, D=223, L=5
I=0336 C=0333 P=00f9, D=570, L=3
I=033a C=0337 P=0218, D=287, L=3
I=033f C=0326 P=02b4, D=114, L=25
I=0340 C=0326 P=0278, D=174, L=26
----
I=034c C=0349 P=009a, D=687, L=3
I=0355 C=0341 P=02d1, D=112, L=20
I=0356 C=0341 P=0307, D=58, L=21
----
I=035a C=0357 P=0241, D=278, L=3
I=035b C=0358 P=02aa, D=174, L=3
----
I=036e C=036b P=009a, D=721, L=3
I=0377 C=0363 P=02d1, D=146, L=20
I=0378 C=0363 P=0341, D=34, L=21
----
I=037d C=037a P=0083, D=759, L=3
----
I=038b C=0388 P=018e, D=506, L=3
----
I=0394 C=0391 P=02e9, D=168, L=3
----
I=03ba C=03b7 P=009a, D=797, L=3
I=03c3 C=03ae P=0292, D=284, L=21
I=03c4 C=03af P=0363, D=76, L=21
----
I=03c8 C=03c4 P=0081, D=835, L=4
----
I=03cf C=03cc P=0084, D=840, L=3
----
I=03d6 C=03d3 P=0190, D=579, L=3
I=03d7 C=03d4 P=0333, D=161, L=3
----
I=03dc C=03d9 P=0059, D=896, L=3
I=03de C=03db P=0326, D=181, L=3
----
Processing 77.371 seconds.
Source 998 bytes.
Result 0 bytes.
Ratio 100.00%
bruce_dev /> Don’t let the execution times scare you. Remember we are just bread-boarding this in Java and this is running on the JNIOR after all.
So at those points where we would generate compressed output when there is only one match our task is obvious. But what about when there is more than one?
Look closely these matches overlap! That means that if we had acted on the first one we may have missed the opportunity to employ one that follows which sometimes would be a serious improvement. This is the benefit of performing the lazy matches.
There are some cases where there are several usable sequences for a block. We need logic now to select one or more of those sequences so as to end up with the absolute minimum length of generated compressed data. It is not just taking the one longest as there could be two or more that do not overlap but that would result in the optimum outcome. This requires a little examination…
For example in this case:
I=009b C=0098 P=0093, D=5, L=3 I=009d C=009a P=0074, D=38, L=3 ----
If we replace 3 bytes at position 0x98 with [D=5, L=3] that will conflict with data for 0x9a and that second match would be unusable. But in this case since both matches are L=3 we really have no choice but to use only one. Here we need to select the one with the shorter distance (D=5) as that would benefit likely the most from the Huffman coding yet to come.
The following case is a little more interesting:
I=00d2 C=00cf P=009a, D=53, L=3 I=00dc C=00c7 P=006c, D=91, L=21 ----
Here we see that we can replace 21 bytes at 0xc7 with [D=91, L=21] and since this sequence completely contains the other it isn’t needed at all. In this case going with the longest match happens to provide the best compression. But that cannot always be the rule. Here we need to be careful that our algorithm just doesn’t blindly go for the first replacement.
A little further into the file we have this case:
I=0149 C=0146 P=009a, D=172, L=3 I=0152 C=013e P=00c7, D=119, L=20 I=0153 C=013e P=010d, D=49, L=21 ----
Here the longest is again the most beneficial as it completely overlaps the other two.
How about this one?
I=0175 C=0172 P=009a, D=216, L=3 I=017e C=0167 P=002c, D=315, L=23 I=017f C=016a P=013e, D=44, L=21 ----
The 2nd and 3rd matches both eliminate the usefulness of the 1st. The 2nd replaces 23 bytes from addresses 0x167 thru 0x17d inclusive. The 3rd replaces 21 bytes from 0x16a thru 0x17e inclusive. There is not a complete overlap but since we still have to choose one over the other the longer one is the most beneficial.
You can see how we might benefit from some careful implementation here. We do have some flexibility to partially implement one or both of the sequences.
Look at this case that occurs further into the file:
I=0250 C=024d P=00a6, D=423, L=3 I=0251 C=024e P=0068, D=486, L=3 I=0258 C=0255 P=0129, D=300, L=3 I=0267 C=0264 P=009a, D=458, L=3 I=0270 C=0252 P=01b5, D=157, L=30 I=0271 C=0250 P=021f, D=49, L=33 ----
We should elect to use the first to replace bytes from 0x24d thru 0x24f inclusive with [D=423, L=3]. We then should use the 6th to replace bytes from 0x250 thru 0x270 inclusive with [D=49, L=33]. Thus we replace a total of 36 bytes with two references.
Okay, time to create some logic.
To help visualize I added a little plotting. I found this case as an example of partially applying a match.
I=0327 C=0323 P=01dd, D=326, L=4
I=032b C=0326 P=0247, D=223, L=5
I=0336 C=0333 P=00f9, D=570, L=3
I=033a C=0337 P=0218, D=287, L=3
I=033f C=0326 P=02b4, D=114, L=25
I=0340 C=0326 P=0278, D=174, L=26
0323 - 0340
|--|
|---|
|-|
|-|
|-----------------------|
|------------------------|
We can see from this that we can replace the entire range from 0x323 to 0x340 using two sequences.
One option is to truncate the 1st using only 3 of its 4 bytes along with the 6th sequence in its entirety. Remember that the minimum sequence is 3 bytes so we can do this. The replacement being [D=326, L=3][D=174, L=26].
The other option, which we would have to use if the 1st were only 3 bytes, is to use the 1st match and then skip the first byte of the 6th. The replacement then being [D=326, L=4][D=173, L=25].
Is one preferential over the other? I am not sure. This might come down to how the logic is implemented. This is fun though.
Here’s the jniorboot.log run with the sequences plotted if you are interested.
bruce_dev /> cat jniorboot.log -h
00000000 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 01/04/18 .08:19:1
00000010 38 2e 31 31 31 2c 20 2a 2a 20 4f 53 20 43 52 43 8.111,.* *.OS.CRC
00000020 20 64 65 74 61 69 6c 20 75 70 64 61 74 65 64 0d .detail. updated.
00000030 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a .01/04/1 8.08:19:
00000040 31 38 2e 31 35 38 2c 20 2d 2d 20 4d 6f 64 65 6c 18.158,. --.Model
00000050 20 34 31 30 20 76 31 2e 36 2e 33 20 2d 20 4a 41 .410.v1. 6.3.-.JA
00000060 4e 4f 53 20 53 65 72 69 65 73 20 34 0d 0a 30 31 NOS.Seri es.4..01
00000070 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e /04/18.0 8:19:18.
00000080 31 37 38 2c 20 43 6f 70 79 72 69 67 68 74 20 28 178,.Cop yright.(
00000090 63 29 20 32 30 31 32 2d 32 30 31 38 20 49 4e 54 c).2012- 2018.INT
000000A0 45 47 20 50 72 6f 63 65 73 73 20 47 72 6f 75 70 EG.Proce ss.Group
000000B0 2c 20 49 6e 63 2e 2c 20 47 69 62 73 6f 6e 69 61 ,.Inc.,. Gibsonia
000000C0 20 50 41 20 55 53 41 0d 0a 30 31 2f 30 34 2f 31 .PA.USA. .01/04/1
000000D0 38 20 30 38 3a 31 39 3a 31 38 2e 31 39 37 2c 20 8.08:19: 18.197,.
000000E0 4a 41 4e 4f 53 20 77 72 69 74 74 65 6e 20 61 6e JANOS.wr itten.an
000000F0 64 20 64 65 76 65 6c 6f 70 65 64 20 62 79 20 42 d.develo ped.by.B
00000100 72 75 63 65 20 43 6c 6f 75 74 69 65 72 0d 0a 30 ruce.Clo utier..0
00000110 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 1/04/18. 08:19:18
00000120 2e 32 31 36 2c 20 53 65 72 69 61 6c 20 4e 75 6d .216,.Se rial.Num
00000130 62 65 72 3a 20 36 31 34 30 37 30 35 30 30 0d 0a ber:.614 070500..
00000140 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 01/04/18 .08:19:1
00000150 38 2e 32 33 36 2c 20 46 69 6c 65 20 53 79 73 74 8.236,.F ile.Syst
00000160 65 6d 20 6d 6f 75 6e 74 65 64 0d 0a 30 31 2f 30 em.mount ed..01/0
00000170 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e 32 35 4/18.08: 19:18.25
00000180 37 2c 20 52 65 67 69 73 74 72 79 20 6d 6f 75 6e 7,.Regis try.moun
00000190 74 65 64 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 ted..01/ 04/18.08
000001A0 3a 31 39 3a 31 38 2e 33 30 36 2c 20 4e 65 74 77 :19:18.3 06,.Netw
000001B0 6f 72 6b 20 49 6e 69 74 69 61 6c 69 7a 65 64 0d ork.Init ialized.
000001C0 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a .01/04/1 8.08:19:
000001D0 31 38 2e 33 32 36 2c 20 45 74 68 65 72 6e 65 74 18.326,. Ethernet
000001E0 20 41 64 64 72 65 73 73 3a 20 39 63 3a 38 64 3a .Address :.9c:8d:
000001F0 31 61 3a 30 30 3a 30 37 3a 65 65 0d 0a 30 31 2f 1a:00:07 :ee..01/
00000200 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e 34 04/18.08 :19:18.4
00000210 34 37 2c 20 53 65 6e 73 6f 72 20 50 6f 72 74 20 47,.Sens or.Port.
00000220 69 6e 69 74 69 61 6c 69 7a 65 64 0d 0a 30 31 2f initiali zed..01/
00000230 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e 35 04/18.08 :19:18.5
00000240 30 32 2c 20 49 2f 4f 20 73 65 72 76 69 63 65 73 02,.I/O. services
00000250 20 69 6e 69 74 69 61 6c 69 7a 65 64 0d 0a 30 31 .initial ized..01
00000260 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a 31 38 2e /04/18.0 8:19:18.
00000270 35 33 35 2c 20 46 54 50 20 73 65 72 76 65 72 20 535,.FTP .server.
00000280 65 6e 61 62 6c 65 64 20 66 6f 72 20 70 6f 72 74 enabled. for.port
00000290 20 32 31 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 .21..01/ 04/18.08
000002A0 3a 31 39 3a 31 38 2e 35 35 36 2c 20 50 72 6f 74 :19:18.5 56,.Prot
000002B0 6f 63 6f 6c 20 73 65 72 76 65 72 20 65 6e 61 62 ocol.ser ver.enab
000002C0 6c 65 64 20 66 6f 72 20 70 6f 72 74 20 39 32 30 led.for. port.920
000002D0 30 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 0..01/04 /18.08:1
000002E0 39 3a 31 38 2e 35 38 36 2c 20 57 65 62 53 65 72 9:18.586 ,.WebSer
000002F0 76 65 72 20 65 6e 61 62 6c 65 64 20 66 6f 72 20 ver.enab led.for.
00000300 70 6f 72 74 20 38 30 0d 0a 30 31 2f 30 34 2f 31 port.80. .01/04/1
00000310 38 20 30 38 3a 31 39 3a 31 38 2e 36 30 38 2c 20 8.08:19: 18.608,.
00000320 54 65 6c 6e 65 74 20 73 65 72 76 65 72 20 65 6e Telnet.s erver.en
00000330 61 62 6c 65 64 20 66 6f 72 20 70 6f 72 74 20 32 abled.fo r.port.2
00000340 33 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 3..01/04 /18.08:1
00000350 39 3a 31 38 2e 36 33 32 2c 20 50 4f 52 3a 20 35 9:18.632 ,.POR:.5
00000360 39 32 36 0d 0a 30 31 2f 30 34 2f 31 38 20 30 38 926..01/ 04/18.08
00000370 3a 31 39 3a 31 38 2e 36 35 33 2c 20 43 75 6d 75 :19:18.6 53,.Cumu
00000380 6c 61 74 69 76 65 20 52 75 6e 74 69 6d 65 3a 20 lative.R untime:.
00000390 38 20 57 65 65 6b 73 20 35 20 44 61 79 73 20 31 8.Weeks. 5.Days.1
000003A0 20 48 6f 75 72 20 32 34 3a 33 32 2e 32 38 31 0d .Hour.24 :32.281.
000003B0 0a 30 31 2f 30 34 2f 31 38 20 30 38 3a 31 39 3a .01/04/1 8.08:19:
000003C0 31 38 2e 36 37 38 2c 20 42 6f 6f 74 20 43 6f 6d 18.678,. Boot.Com
000003D0 70 6c 65 74 65 64 20 5b 32 2e 33 20 73 65 63 6f pleted.[ 2.3.seco
000003E0 6e 64 73 5d 0d 0a nds]..
bruce_dev />bruce_dev /> jtest jniorboot.log
I=0044 C=0031 P=0000, D=49, L=19
0031 - 0044
|-----------------|
I=0064 C=0061 P=001a, D=71, L=3
0061 - 0064
|-|
I=0081 C=006c P=002f, D=61, L=21
006c - 0081
|-------------------|
I=0086 C=0082 P=0045, D=61, L=3
0082 - 0085
|-|
I=009d C=0098 P=0093, D=5, L=3
I=009d C=009a P=0074, D=38, L=3
0098 - 009d
|-|
|-|
I=00dd C=00cf P=009a, D=53, L=3
I=00dd C=00c7 P=006c, D=91, L=21
00c7 - 00dc
|-|
|-------------------|
I=00e6 C=00df P=005d, D=130, L=7
00df - 00e6
|-----|
I=00f4 C=00f1 P=0020, D=209, L=3
00f1 - 00f4
|-|
I=0121 C=0115 P=009a, D=123, L=3
I=0121 C=010d P=00c7, D=70, L=20
010d - 0121
|-|
|------------------|
I=012b C=0125 P=0063, D=194, L=5
0125 - 012a
|---|
I=0153 C=0146 P=009a, D=172, L=3
I=0153 C=013e P=00c7, D=119, L=20
I=0153 C=013e P=010d, D=49, L=21
013e - 0153
|-|
|------------------|
|-------------------|
I=0157 C=0154 P=0123, D=49, L=3
0154 - 0157
|-|
I=017f C=0172 P=009a, D=216, L=3
I=017f C=0167 P=002c, D=315, L=23
I=017f C=016a P=013e, D=44, L=21
0167 - 017f
|-|
|---------------------|
|-------------------|
I=0183 C=0180 P=00dd, D=163, L=3
0180 - 0183
|-|
I=01a8 C=019b P=009a, D=257, L=3
I=01a8 C=018b P=0162, D=41, L=28
018b - 01a7
|-|
|--------------------------|
I=01ad C=01a9 P=0154, D=85, L=3
01a9 - 01ac
|-|
I=01bb C=01b3 P=00b1, D=258, L=3
I=01bb C=01b8 P=0129, D=143, L=3
01b3 - 01bb
|-|
|-|
I=01d4 C=01c7 P=009a, D=301, L=3
I=01d4 C=01bd P=0168, D=85, L=22
I=01d4 C=01bd P=0191, D=44, L=23
01bd - 01d4
|-|
|--------------------|
|---------------------|
I=01d8 C=01d5 P=01a9, D=44, L=3
01d5 - 01d8
|-|
I=01e8 C=01e5 P=00a7, D=318, L=3
01e5 - 01e8
|-|
I=020f C=0203 P=009a, D=361, L=3
I=020f C=01fb P=01bf, D=60, L=20
01fb - 020f
|-|
|------------------|
I=0217 C=0211 P=0180, D=145, L=3
I=0217 C=0212 P=0124, D=238, L=4
0211 - 0216
|-|
|--|
I=023f C=0224 P=0129, D=251, L=3
I=023f C=0233 P=009a, D=409, L=3
I=023f C=0221 P=01b5, D=108, L=30
0221 - 023f
|-|
|-|
|----------------------------|
I=0245 C=0242 P=00b0, D=402, L=3
0242 - 0245
|-|
I=0271 C=024d P=00a6, D=423, L=3
I=0271 C=024e P=0068, D=486, L=3
I=0271 C=0255 P=0129, D=300, L=3
I=0271 C=0264 P=009a, D=458, L=3
I=0271 C=0252 P=01b5, D=157, L=30
I=0271 C=0250 P=021f, D=49, L=33
024d - 0271
|-|
|-|
|-|
|-|
|----------------------------|
|-------------------------------|
I=0276 C=0273 P=0155, D=286, L=3
0273 - 0276
|-|
I=0280 C=0278 P=0247, D=49, L=5
0278 - 027d
|---|
I=0288 C=0285 P=00f9, D=396, L=3
0285 - 0288
|-|
I=028c C=0289 P=0218, D=113, L=3
0289 - 028c
|-|
I=0293 C=028d P=021c, D=113, L=4
028d - 0291
|--|
I=02a8 C=029b P=009a, D=513, L=3
I=02a8 C=0293 P=01fb, D=152, L=20
I=02a8 C=0293 P=025c, D=55, L=21
0293 - 02a8
|-|
|------------------|
|-------------------|
I=02af C=02a9 P=01d5, D=212, L=3
I=02af C=02ab P=00a2, D=521, L=4
02a9 - 02af
|-|
|--|
I=02ce C=02b4 P=0247, D=109, L=5
I=02ce C=02c1 P=00f9, D=456, L=3
I=02ce C=02c5 P=0218, D=173, L=3
I=02ce C=02b4 P=0278, D=60, L=25
02b4 - 02cd
|---|
|-|
|-|
|-----------------------|
I=02e7 C=02d9 P=009a, D=575, L=3
I=02e7 C=02cf P=013c, D=403, L=22
I=02e7 C=02d1 P=0293, D=62, L=21
02cf - 02e6
|-|
|--------------------|
|-------------------|
I=02ea C=02e7 P=02a9, D=62, L=3
02e7 - 02ea
|-|
I=0305 C=02ed P=0126, D=455, L=3
I=0305 C=02ee P=0249, D=165, L=3
I=0305 C=02f9 P=00f9, D=512, L=3
I=0305 C=02fd P=0218, D=229, L=3
I=0305 C=02ee P=02b6, D=56, L=23
02ed - 0305
|-|
|-|
|-|
|-|
|---------------------|
I=031c C=030f P=009a, D=629, L=3
I=031c C=0306 P=02d0, D=54, L=21
0306 - 031b
|-|
|-------------------|
I=0320 C=031d P=0082, D=667, L=3
031d - 0320
|-|
I=0341 C=0323 P=01dd, D=326, L=4
I=0341 C=0326 P=0247, D=223, L=5
I=0341 C=0333 P=00f9, D=570, L=3
I=0341 C=0337 P=0218, D=287, L=3
I=0341 C=0326 P=02b4, D=114, L=25
I=0341 C=0326 P=0278, D=174, L=26
0323 - 0340
|--|
|---|
|-|
|-|
|-----------------------|
|------------------------|
I=0356 C=0349 P=009a, D=687, L=3
I=0356 C=0341 P=02d1, D=112, L=20
I=0356 C=0341 P=0307, D=58, L=21
0341 - 0356
|-|
|------------------|
|-------------------|
I=035b C=0357 P=0241, D=278, L=3
I=035b C=0358 P=02aa, D=174, L=3
0357 - 035b
|-|
|-|
I=0378 C=036b P=009a, D=721, L=3
I=0378 C=0363 P=02d1, D=146, L=20
I=0378 C=0363 P=0341, D=34, L=21
0363 - 0378
|-|
|------------------|
|-------------------|
I=037d C=037a P=0083, D=759, L=3
037a - 037d
|-|
I=038c C=0388 P=018e, D=506, L=3
0388 - 038b
|-|
I=0395 C=0391 P=02e9, D=168, L=3
0391 - 0394
|-|
I=03c4 C=03b7 P=009a, D=797, L=3
I=03c4 C=03ae P=0292, D=284, L=21
I=03c4 C=03af P=0363, D=76, L=21
03ae - 03c4
|-|
|-------------------|
|-------------------|
I=03c9 C=03c4 P=0081, D=835, L=4
03c4 - 03c8
|--|
I=03cf C=03cc P=0084, D=840, L=3
03cc - 03cf
|-|
I=03d7 C=03d3 P=0190, D=579, L=3
I=03d7 C=03d4 P=0333, D=161, L=3
03d3 - 03d7
|-|
|-|
I=03de C=03d9 P=0059, D=896, L=3
I=03de C=03db P=0326, D=181, L=3
03d9 - 03de
|-|
|-|
Processing 80.766 seconds.
Source 998 bytes.
Result 0 bytes.
Ratio 100.00%
bruce_dev />I think the first step is to filter out sequences that are completely covered by another. That seems to happen a lot.
I have filtered matched sequences that are eclipsed by another in the block. Since we know what to do when only one sequence remains (just use it) I filtered those from the output. So we are left with overlapping situations that remain to be studied.
bruce_dev /> jtest jniorboot.log
I=009d C=0098 P=0093, D=5, L=3
I=009d C=009a P=0074, D=38, L=3
0098 - 009d
|-|
|-|
I=017f C=0167 P=002c, D=315, L=23
I=017f C=016a P=013e, D=44, L=21
0167 - 017f
|---------------------|
|-------------------|
I=01bb C=01b3 P=00b1, D=258, L=3
I=01bb C=01b8 P=0129, D=143, L=3
01b3 - 01bb
|-|
|-|
I=0217 C=0211 P=0180, D=145, L=3
I=0217 C=0212 P=0124, D=238, L=4
0211 - 0216
|-|
|--|
I=0271 C=024d P=00a6, D=423, L=3
I=0271 C=024e P=0068, D=486, L=3
I=0271 C=0250 P=021f, D=49, L=33
024d - 0271
|-|
|-|
|-------------------------------|
I=02af C=02a9 P=01d5, D=212, L=3
I=02af C=02ab P=00a2, D=521, L=4
02a9 - 02af
|-|
|--|
I=02e7 C=02cf P=013c, D=403, L=22
I=02e7 C=02d1 P=0293, D=62, L=21
02cf - 02e6
|--------------------|
|-------------------|
I=0305 C=02ed P=0126, D=455, L=3
I=0305 C=02ee P=02b6, D=56, L=23
02ed - 0305
|-|
|---------------------|
I=0341 C=0323 P=01dd, D=326, L=4
I=0341 C=0326 P=0278, D=174, L=26
0323 - 0340
|--|
|------------------------|
I=035b C=0357 P=0241, D=278, L=3
I=035b C=0358 P=02aa, D=174, L=3
0357 - 035b
|-|
|-|
I=03c4 C=03ae P=0292, D=284, L=21
I=03c4 C=03af P=0363, D=76, L=21
03ae - 03c4
|-------------------|
|-------------------|
I=03d7 C=03d3 P=0190, D=579, L=3
I=03d7 C=03d4 P=0333, D=161, L=3
03d3 - 03d7
|-|
|-|
I=03de C=03d9 P=0059, D=896, L=3
I=03de C=03db P=0326, D=181, L=3
03d9 - 03de
|-|
|-|
Processing 78.368 seconds.
Source 998 bytes.
Result 0 bytes.
Ratio 100.00%
bruce_dev />There is one block where the remaining matches are mutually exclusive. It is also obvious what to do for that but I would still need to identify it. Maybe the goal is to reduce the sequence set to one but if you cannot then to get to a set of mutually exclusive matches.
Added a step to force mutual exclusivity. The logic now appears as follows:
// Our LZ77 compression engine
static void do_compress(BufferedWriter outfile, BufferedReader infile) throws Throwable {
boolean bFound = false;
// process uncompressed stream
while (infile.ready()) {
// obtain next byte
int ch = infile.read();
//System.out.print((char)ch);
// process active Match objects
Match best = null;
for (int n = SEQ.size() - 1; 0 <= n; n--) { Match m = SEQ.get(n); if (!m.check(ch)) { if (m.len >= 3) {
if (best == null)
best = m;
else if (m.len > best.len)
best = m;
else if (m.len == best.len && m.distance < best.distance)
best = m;
}
SEQ.remove(n);
}
}
if (best != null) {
REPL.add(best);
bFound = true;
}
if (bFound && SEQ.size() == 0) {
// filter out sequences eclipsed by another
for (int n = REPL.size() - 1; 0 <= n; n--) {
Match mn = REPL.get(n);
int k;
for (k = REPL.size() - 1; 0 <= k; k--) { if (k == n) continue; Match mk = REPL.get(k); if (mn.curptr >= mk.curptr && mn.curptr + mn.len <= mk.curptr + mk.len)
break;
}
if (0 <= k)
REPL.remove(n);
}
// Force mutual exclusivity. Note that REPL at this point has matchin SEQ with
// increasing CURPTR.
for (int n = 0; n < REPL.size() - 1; n++) {
Match n1 = REPL.get(n);
Match n2 = REPL.get(n + 1);
if (n2.curptr < n1.curptr + n1.len) {
int adj = n1.curptr + n1.len - n2.curptr;
if (n2.len - adj < 3) REPL.remove(n2); else { n2.curptr += adj; if (n2.curptr >= WINDOW)
n2.curptr -= WINDOW;
n2.ptr += adj;
if (n2.ptr >= WINDOW)
n2.ptr -= WINDOW;
n2.distance -= adj;
n2.len -= adj;
}
}
}
// $ - temporary only display when there are still choices
if (REPL.size() > 1) {
// determine the overall affected range
int start = 0;
int end = 0;
for (int n = 0; n < REPL.size(); n++) {
Match m = REPL.get(n);
System.out.printf("I=%04x C=%04x P=%04x, D=%d, L=%d\n",
INPTR, m.curptr, m.start, m.distance, m.len);
if (n == 0 || m.curptr < start) start = m.curptr; if (n == 0 || m.curptr + m.len > end)
end = m.curptr + m.len;
}
// plot
System.out.printf("%04x - %04x\n", start, end);
for (int n = 0; n < REPL.size(); n++) {
Match m = REPL.get(n);
for (int i = start; i <= end; i++) {
if (i < m.curptr || i >= m.curptr + m.len)
System.out.print(" ");
else if (i == m.curptr || i == m.curptr + m.len - 1)
System.out.print("|");
else
System.out.print("-");
}
System.out.println("");
}
System.out.println("");
}
REPL.clear();
bFound = false;
}
// queue uncompressed DATA
As matches are located we select the best (lines 14 thru 29) and add them to a list (lines 30 thru 33). Then later when we reach that point where there are no more active matches and we can generate compressed output (line 35) we filter those eclipsed sequences (lines 38 thru 52). Next we force the remaining sequences to be mutually exclusive (lines 56 thru 74).
Since these sequences appear in the REPL list in increasing CURPTR order (at least they appear to be) we take pairs of sequences and shift the starting point of the next one so it no longer overlaps. If this shrinks the match to less than 3 bytes it is removed.
After that there is code to display and plot the remaining sequences if there are more than one. Here we see that in every case we have created a mutually exclusive set.
bruce_dev /> jtest jniorboot.log
I=01bb C=01b3 P=00b1, D=258, L=3
I=01bb C=01b8 P=0129, D=143, L=3
01b3 - 01bb
|-|
|-|
I=0271 C=024d P=00a6, D=423, L=3
I=0271 C=0250 P=021f, D=49, L=33
024d - 0271
|-|
|-------------------------------|
I=02af C=02a9 P=01d5, D=212, L=3
I=02af C=02ac P=00a2, D=520, L=3
02a9 - 02af
|-|
|-|
I=0305 C=02ed P=0126, D=455, L=3
I=0305 C=02f0 P=02b6, D=54, L=21
02ed - 0305
|-|
|-------------------|
I=0341 C=0323 P=01dd, D=326, L=4
I=0341 C=0327 P=0278, D=173, L=25
0323 - 0340
|--|
|-----------------------|
Processing 77.415 seconds.
Source 998 bytes.
Result 0 bytes.
Ratio 100.00%
bruce_dev /> So it would appear now that I have what I need to generate the compressed output stream.
Generating the compressed output using the [D=,L=] format just to make things visible actually enlarges the file of course. But here it is (some line breaks at the right margin manually inserted).
bruce_dev /> cat outfile.dat 01/04/18 08:19:18.111, ** OS CRC detail updated [D=49,L=19]58, -- Model 410 v1.6.3 - JAN[D=71,L=3]Series 4[D=61,L=21]7[D=61,L=3]Copyright (c) 2012-[D=5,L=3]8 INTEG Process Group, Inc., Gibsonia PA USA[D=91,L=21]97,[D=130,L=7]written and[D=209,L=3]veloped by Bruce Cl outier[D=70,L=20]216,[D=194,L=5]al Number: 614070500[D=49,L=21]3[D=49,L=3]File System moun[D=315,L=23]25[D=16 3,L=3]Registry[D=41,L=28]30[D=85,L=3]Network[D=258,L=3]it[D=143,L=3]iz[D=44,L=23]2[D=44,L=3]Ethernet Addr[D=3 18,L=3]: 9c:8d:1a:00:07:ee[D=60,L=20]44[D=145,L=3]Sensor Port i[D=108,L=30]502[D=402,L=3]/O servi[D=423,L=3][ D=49,L=33]35[D=286,L=3]TP[D=49,L=5]er enabl[D=396,L=3]f[D=113,L=3]p[D=113,L=4]21[D=55,L=21]5[D=212,L=3][D=520 ,L=3]tocol[D=60,L=25]92[D=403,L=22]58[D=62,L=3]Web[D=455,L=3][D=54,L=21]8[D=54,L=21]60[D=667,L=3]Tel[D=326,L= 4][D=173,L=25]3[D=58,L=21]3[D=278,L=3]POR: 5926[D=34,L=21]53[D=759,L=3]umulative R[D=506,L=3]ime: 8[D=168,L=3 ]eks 5 Days 1 Hour 24:32.28[D=284,L=21]6[D=835,L=4]Boot[D=840,L=3]mple[D=579,L=3] [2[D=896,L=3]seconds] bruce_dev />
So it appears to be time to convert this into a bit stream with the proper length and distance codes in preparation for Huffman coding.
Sticking in a couple of placeholder bytes for the length and distance codes this is representative of the pre-Huffman coding compression ratio of this file.
bruce_dev /> jtest jniorboot.log Processing 79.124 seconds. Source 998 bytes. Result 533 bytes. Ratio 46.59% bruce_dev />
Oh it’ll be fast in C and in the JANOS kernel. Okay… Huffman.
So before getting too deep into generating the Huffman coding with dynamic tables I figured that it would make sense to write a quick decompressor for my interim LZ77 compression as a check. I modified the compressor to output length and distance codes as shorts using a 0xff prefix which I then escaped. This stream I will later be able to digest in performing the Huffman coding. The decompressor would take outfile.dat and generate the decompressed newfile.dat.
Well after compressing and then decompressing the content of newfile.dat resembled jniorboot.log very closely but there were a few variances. First, I found the glitch in the step that eliminates any overlap in matched sequences (shouldn’t have modified distance when also modifying the CURPTR). Then I had to address the boundary conditions at the end of the file in order to properly process the entire file (I ended up a couple of bytes short initially). With that we achieved success.
You can see here how we can use MANIFEST to verify file size and content. Note that the MD5 are identical.
bruce_dev /> jtest jniorboot.log Processing 69.323 seconds. Source 950 bytes. Result 671 bytes. Ratio 1.42:1 bruce_dev /> jtest2 bruce_dev /> manifest jniorboot.log JNIOR Manifest Fri Jan 05 11:02:57 EST 2018 Size MD5 File Specification 950 dc425a0283e22944b463eeab9e625adb [Modified] /jniorboot.log End of Manifest (1 files listed) bruce_dev /> manifest newfile.dat JNIOR Manifest Fri Jan 05 11:02:59 EST 2018 Size MD5 File Specification 950 dc425a0283e22944b463eeab9e625adb [New] /newfile.dat End of Manifest (1 files listed) bruce_dev />
Here is the original content and the resulting compressed format that I have used in bread-boarding this.
bruce_dev /> cat jniorboot.log
01/05/18 07:39:52.913, -- Model 410 v1.6.3 - JANOS Series 4
01/05/18 07:39:52.960, Copyright (c) 2012-2018 INTEG Process Group, Inc., Gibsonia PA USA
01/05/18 07:39:52.980, JANOS written and developed by Bruce Cloutier
01/05/18 07:39:52.999, Serial Number: 614070500
01/05/18 07:39:53.018, File System mounted
01/05/18 07:39:53.039, Registry mounted
01/05/18 07:39:53.089, Network Initialized
01/05/18 07:39:53.109, Ethernet Address: 9c:8d:1a:00:07:ee
01/05/18 07:39:53.229, Sensor Port initialized
01/05/18 07:39:53.284, I/O services initialized
01/05/18 07:39:53.327, FTP server enabled for port 21
01/05/18 07:39:53.347, Protocol server enabled for port 9200
01/05/18 07:39:53.368, WebServer enabled for port 80
01/05/18 07:39:53.390, Telnet server enabled for port 23
01/05/18 07:39:53.414, POR: 5927
01/05/18 07:39:53.439, Cumulative Runtime: 8 Weeks 5 Days 9 Hours 32:22.102
01/05/18 07:39:53.460, Boot Completed [2.3 seconds]
bruce_dev />bruce_dev /> cat outfile.dat -h
00000000 30 31 2f 30 35 2f 31 38 20 30 37 3a 33 39 3a 35 01/05/18 .07:39:5
00000010 32 2e 39 31 33 2c 20 2d 2d 20 4d 6f 64 65 6c 20 2.913,.- -.Model.
00000020 34 31 30 20 76 31 2e 36 2e 33 20 2d 20 4a 41 4e 410.v1.6 .3.-.JAN
00000030 4f 53 20 53 65 72 69 65 73 20 34 0d 0a ff 00 13 OS.Serie s.4.....
00000040 00 3d 36 30 2c 20 43 6f 70 79 72 69 67 68 74 20 .=60,.Co pyright.
00000050 28 63 29 20 32 30 31 32 2d ff 00 03 00 05 38 20 (c).2012 -.....8.
00000060 49 4e 54 45 47 20 50 72 6f 63 65 73 73 20 47 72 INTEG.Pr ocess.Gr
00000070 6f 75 70 2c 20 49 6e 63 2e 2c 20 47 69 62 73 6f oup,.Inc .,.Gibso
00000080 6e 69 61 20 50 41 20 55 53 41 ff 00 15 00 5b 38 nia.PA.U SA....[8
00000090 ff 00 03 00 5b ff 00 06 00 82 77 72 69 74 74 65 ....[... ..writte
000000A0 6e 20 61 6e 64 20 64 65 76 65 6c 6f 70 65 64 20 n.and.de veloped.
000000B0 62 79 20 42 72 75 63 65 20 43 6c 6f 75 74 69 65 by.Bruce .Cloutie
000000C0 72 ff 00 15 00 46 39 39 2c ff 00 05 00 c2 61 6c r....F99 ,.....al
000000D0 20 4e 75 6d 62 65 72 3a 20 36 31 34 30 37 30 35 .Number: .6140705
000000E0 30 30 ff 00 12 00 31 33 2e ff 00 03 00 b9 2c 20 00....13 ......,.
000000F0 46 69 6c 65 20 53 79 73 74 65 6d 20 6d 6f 75 6e File.Sys tem.moun
00000100 74 65 64 ff 00 15 00 2c 33 ff 00 03 00 5d 52 65 ted...., 3....]Re
00000110 67 69 73 74 72 79 ff 00 1d 00 29 38 ff 00 03 00 gistry.. ..)8....
00000120 29 4e 65 74 77 6f 72 6b ff 00 03 01 02 69 74 ff )Network .....it.
00000130 00 03 00 8f 69 7a ff 00 16 00 2c 31 30 ff 00 03 ....iz.. ..,10...
00000140 00 2c 45 74 68 65 72 6e 65 74 20 41 64 64 72 ff .,Ethern et.Addr.
00000150 00 03 01 3e 3a 20 39 63 3a 38 64 3a 31 61 3a 30 ...>:.9c :8d:1a:0
00000160 30 3a ff 00 03 00 2c 65 65 ff 00 14 00 3c 32 32 0:....,e e....<22
00000170 ff 00 05 00 ee 6e 73 6f 72 20 50 6f 72 74 20 69 .....nso r.Port.i
00000180 ff 00 1e 00 6c 32 38 34 ff 00 03 01 92 2f 4f 20 ....l284 ...../O.
00000190 73 65 72 76 69 ff 00 03 01 a7 ff 00 20 00 31 33 servi... ......13
000001A0 32 37 ff 00 03 01 1e 54 50 ff 00 05 00 31 65 72 27.....T P....1er
000001B0 20 65 6e 61 62 6c ff 00 03 01 8c 66 ff 00 03 00 .enabl.. ...f....
000001C0 71 70 ff 00 04 00 71 32 31 ff 00 15 00 37 34 ff qp....q2 1....74.
000001D0 00 03 00 37 ff 00 03 02 09 74 6f 63 6f 6c ff 00 ...7.... .tocol..
000001E0 19 00 3c 39 32 ff 00 16 01 93 33 36 ff 00 03 01 ..<92... ..36....
000001F0 93 57 65 62 ff 00 03 01 c7 ff 00 15 00 38 38 ff .Web.... .....88.
00000200 00 16 00 36 39 ff 00 03 02 40 54 65 6c ff 00 04 ...69... .@Tel...
00000210 01 46 ff 00 19 00 ae 33 ff 00 14 00 3a 34 31 ff .F.....3 ....:41.
00000220 00 03 01 16 50 4f 52 3a 20 35 39 32 37 ff 00 15 ....POR: .5927...
00000230 00 22 ff 00 04 01 f9 43 75 6d 75 6c 61 74 69 76 .".....C umulativ
00000240 65 20 52 ff 00 03 01 fa 69 6d 65 3a 20 38 ff 00 e.R..... ime:.8..
00000250 03 00 a8 65 6b 73 20 35 20 44 61 79 73 20 39 20 ...eks.5 .Days.9.
00000260 48 6f 75 72 73 20 33 32 3a 32 32 ff 00 03 01 da Hours.32 :22.....
00000270 32 ff 00 15 00 4d ff 00 04 03 44 42 6f 6f 74 ff 2....M.. ..DBoot.
00000280 00 03 03 49 6d 70 6c 65 ff 00 03 02 44 20 5b 32 ...Imple ....D.[2
00000290 ff 00 03 03 81 73 65 63 6f 6e 64 73 5d 0d 0a .....sec onds]..
bruce_dev />- ATTACHMENTS
-
- JTest2.java
- (3.04 KiB) Downloaded 25 times
-
- JTest.java
- (9.42 KiB) Downloaded 24 times
So at this point I feel like this algorithm generates the optimum LZ77 compression for the data. This should even take into account the lazy matches however that is perceived by the industry. When I cast it into C I will work on optimizing the execution.
The only question might be in optimizing distance codes to minimize extra bits. I didn’t consider that in pruning the matched sequence list for a block. When those situations occur there might be a bit or two to save if I were to retain the closer match. I am not going to worry about that. My feeling is that we son’t save anything noticeable if anything at all.
Now to handle the Huffman coding.
Well there are a couple of bugs in my coding which were discovered while testing the approach on much larger files. With those issues fixed I see that I need to focus on optimizing because this all-encompassing matching is much too slow (even when considering the Java breadboard).
The approach would find all of the sequence matches to data in the previous 32KB of the stream (sliding window) for a section of the input stream bound by non-matching data. Once collected I would then end up trashing the vast majority of those. That is wasteful of processing time. It was a logical approach if without thinking you weren’t sure if a better compression ratio couldn’t be obtained through careful selection of sequences. There is this suggestion that better compression is possible if lazy matches are allowed. Without really knowing what those are the shotgun all-encompassing approach guaranteed at least that you had all of the information you needed to reach the optimum. Let’s actually look at this more closely.
Matching
We start a match upon receipt of a data bytes. I’m keeping a bidirectional linked list for the occurrences of each byte value. This allows the routine to rapidly create an active match object for each. Subsequently as each new byte is received we check each active match for those that may be extended and those that are no longer useful. When we reach a point where none of the active matches have been extended we select the longest match completed as the best. For matches of equal length we pick the closest one (lowest distance).
The DEFLATE specification recognizes matches of 3 or more bytes (maximum 258). Why 3? That is because the compression is achieved by replacing a matched sequence with a pointer back to the same data found in previous 32KB of data (the sliding window). That pointer consists of a distance and a length. That pointer in the worst case requires about 3 bytes. So replacing shorter sequences on average won’t buy you anything. That’s for DEFALTE. I am actually using like 5 bytes for this breadboard but eventually we will be be strictly DEFLATE. Obviously the longer the match the greater the savings. Therefore the best match is the longest and closest (uses a minimum pointer size).
So for a point in the incoming stream we seek the longest match. If there is no 3 byte match then we output that first byte as is and search using the next one. The results can be impressive especially for text and log files. It’s not LZW but it works. It turns out to be good enough for the JNIOR.
Lazy Matching
So what is with this lazy matching? Well imagine a sequence of 3 or more matching bytes located someplace in the sliding window. The consider that if we ignored that match and searched for matches starting with the next byte we might find a much longer match from someplace else in the sliding window. Do we miss an opportunity for better compression?
I can graphically show the overlap of the best matches. Say the first is 5 in lenght and the other some 15.
|---| |-------------|
Here vertical bars denote the first and last matching byte and the dashes bytes in between. The first would replace 5 data bytes and the second 15 starting a byte later.
If we were to strictly process matches as they are found we would encode the 5-byte match. And then we would still find the latter 11 bytes of the seconds sequence (or maybe even another better sequence). This would encode as two sequences one right after another and require two pointers for a total of maybe 6 bytes.
|---||---------| 2 pointers = 6 bytes
Note that we can always prune a match. We can ignore some of its leading bytes by incrementing the replace position (CURPTR) and decrementing the length. We can even ignore trailing bytes in a match merely by shortening its length. So here we drop the first 4 bytes of the 15-byte sequence that were eclipsed by the initial 5-byte sequence. We don’t have to actually do this manipulation as supposedly our search algorithm would find it directly for us.
Now those who get excited by such things would point out that if we absolutely ignored the first 5-byte sequence completely and outputted that first raw byte then we would use just one pointer.
.|-------------| 1 raw byte plus 1 pointer = 4 bytes
And, yes, there is a savings that depending on how often such a thing occurs will in fact lead to a better result. This is a lazy match. This is even true when the second sequence is further offset as seen here.
|---| |-------------| ..|-------------| 2 raw bytes plus 1 pointer = 5 bytes
But there is no benefit beyond that. If the two sequences were offset by 3 bytes then you might as well include first 3 as a sequence and you end up using 6 bytes (or less) anyway with 2 pointers.
OK so
Alright for the JNIOR it is likely that these lazy matches aren’t necessary. After all we just want to create a file collection or a graphics file. We aren’t really worried about saving every byte. In fact, we are probably more concerned about it getting done quickly.
So using matches as they come works. But… if we can find a way to efficiently accommodate the lazy matching it would be cool.
Optimized Program Code
Now that I have a little better understanding as to the lazy matching we can take what we have and move on to the next step in DEFLATE. Later after I cast this into C we can decide if it is worth handling the lazy matches. It represents a trade off between an optimum compression ratio and processing time. For the JNIOR we really are more concerned about the processing time as the brute force compression ratios appear more than acceptable. Note that I bet that our original processing of all possible matches between unmatched raw data would lead to an even better compression ratio than that including just the lazy matches but that would be slow.
Speaking of slow I thought to take a little time to distill our algorithm down and to code it so it would execute faster. I know that it is still a breadboard but I would like to not waste as much time with iterations in debugging. So I have eliminated the Match object and automatic growing lists. And since we are identifying the best match for a single position I have eliminated the list of completed matches (RSEQ). I also made an adjustment so as to be able to replay bytes into the matcher should we need to output raw data.
The following is the LZ77 code. Hopefully the comments are sufficient for you to follow the algorithm.
// Our LZ77 compression engine
static void do_compress(BufferedOutputStream outfile, BufferedInputStream infile, int filesize)
throws Throwable {
int ch;
// process uncompressed stream byte-by-byte
while (filesize > 0) {
// Make sure that there are bytes in the queue to work with. We process bytes from
// the queue using SEQPTR. When SEQPTR reaches the INPTR then we add bytes from the input
// stream. The linked lists are updated.
if (SEQPTR == INPTR) {
// obtain byte from uncompressed stream
ch = infile.read();
filesize--;
// queue data and manage associated linked list
DATA[INPTR] = (byte)ch;
// Add byte to the head of the appropriate linked list. Note pointers are stored +1 so
// as to use 0 as an end of list marker. Lists are bi-directional so we can trim the
// tail when data is dropped from the queue.
int ptr = HEAD[ch];
HEAD[ch] = INPTR + 1;
FWD[INPTR] = ptr;
BACK[INPTR] = 0;
if (ptr != 0)
BACK[ptr - 1] = INPTR + 1;
// advance entry pointer
INPTR++;
if (INPTR == WINDOW)
INPTR = 0;
// drop old data from queue when the sliding window is full
if (INPTR == OUTPTR) {
// trim linked list as byte is being dropped
if (BACK[OUTPTR] == 0)
HEAD[DATA[OUTPTR]] = 0;
else
FWD[BACK[OUTPTR] - 1] = 0;
// push end of queue
OUTPTR++;
if (OUTPTR == WINDOW)
OUTPTR = 0;
}
}
// Obtain the next character to process. We are assured of a byte at SEQPTR now.
// SEQPTR allows us to replay bytes into the sequence matching.
ch = DATA[SEQPTR++];
if (SEQPTR == WINDOW)
SEQPTR = 0;
// Reset match state. These will define the best match should one be found for
// the current CURPTR.
int best_distance = 0;
int best_length = 0;
// If there are no active sequences we create a new set. This uses the linked list
// for the byte at CURPTR to initialize a series of potention sequence sites.
if (MSIZE == 0) {
// create new active matches for all CH in the queue (except last)
int ptr = HEAD[ch];
while (ptr != 0) {
if (ptr - 1 != CURPTR) {
int distance = CURPTR - ptr + 1;
if (distance < 0)
distance += WINDOW;
DISTANCE[MSIZE] = distance;
LENGTH[MSIZE] = 1;
MSIZE++;
}
ptr = FWD[ptr - 1];
}
}
// Otherwise process the active sequence matches. Here we advance sequences as each
// new byte is processed. Of those matches that cannot be extended we keep the
// best (longest and closest to CURPTR). We will use the best match if all of the
// potential matches end.
else {
// each active match
for (int n = MSIZE - 1; 0 <= n; n--) {
int p = CURPTR - DISTANCE[n];
if (p < 0) p += WINDOW; p += LENGTH[n]; if (p >= WINDOW)
p -= WINDOW;
// Can we extend this match? If so we bump its length and move on to
// the next match.
if (DATA[p] == ch && LENGTH[n] < 258) {
LENGTH[n]++;
if (DISTANCE[n] + LENGTH[n] < WINDOW && filesize > 0)
continue;
}
// Sequence did not get extended. See if it is the best found so far.
if (LENGTH[n] >= 3) {
// first
if (best_length == 0) {
best_distance = DISTANCE[n];
best_length = LENGTH[n];
}
// longer
else if (LENGTH[n] > best_length) {
best_distance = DISTANCE[n];
best_length = LENGTH[n];
}
// closer
else if (LENGTH[n] == best_length && DISTANCE[n] < best_distance) { best_distance = DISTANCE[n]; best_length = LENGTH[n]; } } // Competed matches are eliminated from the active list. To be quick we // replace it with the last in the list and reduce the count. MSIZE--; DISTANCE[n] = DISTANCE[MSIZE]; LENGTH[n] = LENGTH[MSIZE]; } } // If there are no active sequence matches at this point we can generate output. if (MSIZE == 0) { // If a we have a completed sequence we can output a pointer. These are escaped // into the output buffer for later processing into encoded length-distance // pairs. best_length = 0; if (best_length != 0) { bufwrite(0xff, outfile); bufint(best_length, outfile); bufint(best_distance, outfile); // Move CURPTR to the next byte after the replaced sequence CURPTR += best_length; if (CURPTR >= WINDOW)
CURPTR -= WINDOW;
}
// Otherwise output a raw uncompressed byte. The unmatched byte is sent to
// the output stream and we move CURPTR to the next.
else {
bufbyte(DATA[CURPTR], outfile);
CURPTR++;
if (CURPTR == WINDOW)
CURPTR = 0;
}
// Here we reset SEQPTR to process from the nex CURPTR location. In the case that
// we could not match this replays bytes previously processed so as to not miss
// an opportunity.
SEQPTR = CURPTR;
}
}
// If we are done and there are unprocessed bytes left we push them to the output stream.
while (CURPTR != INPTR) {
bufbyte(DATA[CURPTR], outfile);
CURPTR++;
if (CURPTR == WINDOW)
CURPTR = 0;
}
}
With this in place we are going to move on to see what needs to be done next with our output stream.
Our LZ77 compression routine loads an output buffer with processed and hopefully compressed data. When this output buffer fills (say to 64KB) we must process it further. That data is then compressed again using a form of Huffman coding.
Huffman coding for DEFLATE
If you search you can find lots of useful descriptions of Huffman coding. Not all of those will provide the detail for constructing the required tree from the data. Of those that do, most do not lead you to creating a Huffman table compatible with DEFLATE. This is because the Huffman table in DEFLATE is eventually stored using a form of shorthand. That is only possible if the Huffman encoding follows some addition rules. To meet those requirements we need to be careful in constructing our initial dynamic tree.
The DEFLATE specification cryptically defines it:
The Huffman codes used for each alphabet in "deflate" format have two additional rules:
* All codes of a given bit length have lexicographically consecutive values, in the same order as the
symbols they represet;
* Shorter codes lexicographically precede longer codes.
It would be nice if they would avoid words like lexicographically but you can’t have everything. You can also get confused over the term codes verses the binary values of the bytes in the alphabet. And of course shorter refers to bit count. That being perhaps a little more obvious but here again these must “lexicographically precede” others.
Alphabet
This refers to the set of values that we intend to compress. Obviously this needs to include byte values (0..255) since we are not constraining our input to ASCII or something. We include all of the possible values in the alphabet (in increasing value) even if some do not appear in the data. That seems obvious but DEFLATE also defines an end-of-block code (like an EOF) of 256 as well as special codes from 257..285 used to represent length codes (in the length-distance pointers we created).
So we will need to encode bytes from 0 thru 285. Okay, That set requires 9 bits and makes life in a world of bytes difficult. Remember how I had to escape my length-distance pointers in the buffer? Anyway, we can handle it in building our trees as we can define the value of a node as an integer. So for DEFLATE our “alphabet” consists of the numbers 0..285.
Don’t be confused if you notice that length codes and also distance codes generally include some “extra” bits. They do and those are simply slipped into the bit stream and are not subjected to Huffman coding. We’ll get into that later.
Length codes
These lie outside of the normal byte values 0..255 simply because in decompression we need to recognize them. These are flagged just as I have escaped the same in the output buffer. There are 29 of the length codes which are used with extra bits in some cases to encode lengths of 3 to 258. You may recall that we did not create matching sequences of less that 3 bytes and there is a maximum of a 258 byte length. The 258 maximum I bet results from storing the length-3 as a byte (0..255) someplace. But I would be very curious as to the thought process that breaks these 256 possible lengths into 29 codes. That is likely based upon some probability distribution or some such thing. It is what it is.
Distance codes
Unlike the length codes the distance codes do not need to be flagged. We expect a distance code after a length code and so those use normal byte values already represented in the alphabet (0..29). Here there are 30 distance codes some also requiring extra bits encoding distance from 1..32768. This allows the matched sequence to sit in that 32KB sliding window.
Huffman coding compresses data by representing frequent values with a small number of bits. If a space ' ' (0x20) appears in the data a tremendous number of times it might get encoded by just 2 bits. That saving 6 bits for every occurrence of a space. That can be a huge savings. The down side is that a rare byte that might occur only a few times might be encoded by 10 bits. That actually increases the storage from the original 8-bit byte but happens only a few times.
This implies then that we know the frequencies of each member of our alphabet. That is the first step. We need to proceed to count each occurrence of each member in our alphabet that appears in the data.
Here we modify my bufflush() routine that is responsible for emptying the buffer. First we will add a routine to count. There are 286 members in the alphabet (256 byte values, the end-of-block code and 29 length codes). We create an integer array where we use the value as an index to count occurrences. There is one complication in that I need to convert my length-distance escaping into the DEFLATE encoding. That entails tables of length and distance ranges so we can decide which of the length and distance codes we need to use.
// length code range maximums
static int[] blen = {
4, 5, 6, 7, 8, 9, 10, 11, 13, 15, 17, 19, 23, 27, 31, 35,
43, 51, 59, 67, 83, 99, 115, 131, 163, 195, 227, 258, 259
};
Here for each or the 29 length ranges we specify the largest size plus 1 that it can encode. For a given length we will loop through these ranges to determine the proper alphabet value to use. The DEFLATE lengths are encoded as follows (from RFC 1951):
Extra Extra Extra
Code Bits Length(s) Code Bits Lengths Code Bits Length(s)
---- ---- ------ ---- ---- ------- ---- ---- -------
257 0 3 267 1 15,16 277 4 67-82
258 0 4 268 1 17,18 278 4 83-98
259 0 5 269 2 19-22 279 4 99-114
260 0 6 270 2 23-26 280 4 115-130
261 0 7 271 2 27-30 281 5 131-162
262 0 8 272 2 31-34 282 5 163-194
263 0 9 273 3 35-42 283 5 195-226
264 0 10 274 3 43-50 284 5 227-257
265 1 11,12 275 3 51-58 285 0 258
266 1 13,14 276 3 59-66
Similarly we create an array for the 30 distance codes.
static int[] bdist = {
2, 3, 4, 5, 7, 9, 13, 17, 25, 33, 49, 65, 97, 129, 193,
257, 385, 513, 769, 1025, 1537, 2049, 3073, 4097, 6145,
8193, 12289, 16385, 24577, 32769
};
The DEFLATE specification encodes distances as follows:
Extra Extra Extra
Code Bits Dist Code Bits Dist Code Bits Distance
---- ---- ---- ---- ---- ------ ---- ---- --------
0 0 1 10 4 33-48 20 9 1025-1536
1 0 2 11 4 49-64 21 9 1537-2048
2 0 3 12 5 65-96 22 10 2049-3072
3 0 4 13 5 97-128 23 10 3073-4096
4 1 5,6 14 6 129-192 24 11 4097-6144
5 1 7,8 15 6 193-256 25 11 6145-8192
6 2 9-12 16 7 257-384 26 12 8193-12288
7 2 13-16 17 7 385-512 27 12 12289-16384
8 3 17-24 18 8 513-768 28 13 16385-24576
9 3 25-32 19 8 769-1024 29 13 24577-32768
So this buffer flush routine looks as follows. Note that we are not encoding the output in any way yet. This merely determines the counts.
// length code range maximums
static int[] blen = {
4, 5, 6, 7, 8, 9, 10, 11, 13, 15, 17, 19, 23, 27, 31, 35,
43, 51, 59, 67, 83, 99, 115, 131, 163, 195, 227, 258, 259
};
static int[] bdist = {
2, 3, 4, 5, 7, 9, 13, 17, 25, 33, 49, 65, 97, 129, 193,
257, 385, 513, 769, 1025, 1537, 2049, 3073, 4097, 6145,
8193, 12289, 16385, 24577, 32769
};
static void bufflush(BufferedOutputStream outfile) throws Throwable {
// Determine frequecies by counting each occurrence of a byte value
int[] freq = new int[286];
for (int n = 0; n < BUFPTR; n++) {
// Get the byte value. This may be escaped ith 0xff.
int ch = BUFR[n] & 0xff;
// not escaped
if (ch != 0xff)
freq[ch]++;
// escaped
else {
// Get next byte.
ch = BUFR[++n] & 0xff;
// may just be 0xff itself
if (ch == 0xff)
freq[0xff]++;
// length-distance pair
else {
// obtain balance of length and distance values
int len = (ch << 8) + (BUFR[++n] & 0xff);
int dist = ((BUFR[++n] & 0xff) << 8) + (BUFR[++n] & 0xff);
// determine length code to use (257..285)
for (int k = 0; k < blen.length; k++) {
if (len < blen[k]) {
freq[257 + k]++;
break;
}
}
// determine distance code to use (0..29)
for (int k = 0; k < bdist.length; k++) {
if (dist < bdist[k]) {
freq[k]++;
break;
}
}
}
}
}
// dump the results
for (int n = 0; n < 256; n++) { if (freq[n] > 0)
System.out.printf("0x%03x %d\n", n, freq[n]);
}
And the unsorted results. Here we list only those values that appear in the data.
jtest jniorboot.log
0x004 1
0x00a 9
0x00b 13
0x00c 4
0x00d 5
0x00e 8
0x00f 3
0x010 4
0x011 8
0x012 2
0x013 2
0x020 41
0x028 1
0x029 1
0x02c 6
0x02d 5
0x02e 7
0x02f 3
0x030 16
0x031 12
0x032 12
0x033 6
0x034 10
0x035 7
0x036 6
0x037 4
0x038 9
0x039 9
0x03a 10
0x041 4
0x042 2
0x043 3
0x044 1
0x045 2
0x046 1
0x047 3
0x048 1
0x049 3
0x04a 1
0x04d 1
0x04e 4
0x04f 3
0x050 4
0x052 3
0x053 4
0x054 3
0x055 1
0x057 1
0x05b 1
0x05d 1
0x061 8
0x062 5
0x063 7
0x064 9
0x065 29
0x066 1
0x067 2
0x068 2
0x069 14
0x06b 2
0x06c 10
0x06d 6
0x06e 9
0x06f 17
0x070 5
0x072 17
0x073 11
0x074 15
0x075 8
0x076 4
0x077 2
0x079 5
0x07a 1
0x101 30
0x102 2
0x103 3
0x105 1
0x10c 1
0x10d 13
0x10e 2
0x10f 2
0x110 1
Processing 6.129 seconds.
Source 954 bytes.
Result 680 bytes.
Ratio 1.40:1
bruce_dev /> There is one omission. We will in fact use one end-of-block code (0x100) and so we will need to force it into the table.
I will need to build a tree. So we need to create some kind of node which will have left and right references as well as a potential value and a weigh (frequency). Here I will define a class.
static ArrayList nodes = new ArrayList(512);
static class Node {
int left;
int value;
int weight;
int right;
int length;
int code;
Node() {
}
// instantiate leaf
Node(int val, int w) {
value = val;
weight = w;
}
// instantiate node
Node(int l, int r, int w) {
left = l;
right = r;
weight = w;
}
}
I know that later I will assign individual leaves a code length and a code so those are included in the class as well. Now I will take our array of value frequencies and create leaves for each of those that appear in the data. An ArrayList will store these nodes and grow as we define a full tree.
I will also create an ordering array that we will use to properly constructing the tree. Each entry in this array will reference a node. Initially we will sort this by decreasing frequency. Also in keeping with the lexicographical requirement those nodes of the same frequency will be ordered by increasing alphabet value. This is where it gets tricky but we start here.
We replace the frequency dump loop with the following.
// create node set (0 not used)
int[] order = new int[286];
int cnt = 0;
nodes.add(new Node()); // not used (index 0 is terminator)
for (int n = 0; n < 286; n++) { if (freq[n] > 0) {
nodes.add(new Node(n, freq[n]));
order[cnt++] = nodes.size() - 1;
}
}
// sort
for (int n = 0; n < cnt - 1; n++) {
Node nd1 = nodes.get(order[n]);
Node nd2 = nodes.get(order[n + 1]);
if (nd1.weight < nd2.weight || nd1.weight == nd2.weight && nd1.value > nd2.value) {
int k = order[n];
order[n] = order[n + 1];
order[n + 1] = k;
n -= 2;
if (n < -1)
n = -1;
}
}
//dump
System.out.println("");
for (int n = 0; n < cnt; n++) {
Node nd = nodes.get(order[n]);
System.out.printf("%d 0x%03x %d\n", order[n], nd.value, nd.weight);
}
And the results of the sort are displayed.
bruce_dev /> jtest jniorboot.log
12 0x020 41
75 0x101 30
55 0x065 29
64 0x06f 17
66 0x072 17
19 0x030 16
68 0x074 15
59 0x069 14
3 0x00b 13
80 0x10d 13
20 0x031 12
21 0x032 12
67 0x073 11
23 0x034 10
29 0x03a 10
61 0x06c 10
2 0x00a 9
27 0x038 9
28 0x039 9
54 0x064 9
63 0x06e 9
6 0x00e 8
9 0x011 8
51 0x061 8
69 0x075 8
17 0x02e 7
24 0x035 7
53 0x063 7
15 0x02c 6
22 0x033 6
25 0x036 6
62 0x06d 6
5 0x00d 5
16 0x02d 5
52 0x062 5
65 0x070 5
72 0x079 5
4 0x00c 4
8 0x010 4
26 0x037 4
30 0x041 4
41 0x04e 4
43 0x050 4
45 0x053 4
70 0x076 4
7 0x00f 3
18 0x02f 3
32 0x043 3
36 0x047 3
38 0x049 3
42 0x04f 3
44 0x052 3
46 0x054 3
77 0x103 3
10 0x012 2
11 0x013 2
31 0x042 2
34 0x045 2
57 0x067 2
58 0x068 2
60 0x06b 2
71 0x077 2
76 0x102 2
81 0x10e 2
82 0x10f 2
1 0x004 1
13 0x028 1
14 0x029 1
33 0x044 1
35 0x046 1
37 0x048 1
39 0x04a 1
40 0x04d 1
47 0x055 1
48 0x057 1
49 0x05b 1
50 0x05d 1
56 0x066 1
73 0x07a 1
74 0x100 1
78 0x105 1
79 0x10c 1
83 0x110 1
Processing 8.873 seconds.
Source 954 bytes.
Result 680 bytes.
Ratio 1.40:1
bruce_dev /> The first number if the node index. The next is the value and the last the count of occurrences. Here we see that the space (0x20) is the most frequent in this file. You can see that I included the end-of-block code (0x100) once and it is as infrequent as a few others.
The next step is to construct a Huffman tree. So to simplify things at this point we are going to use a simple phrase as the data and disable the LZ77 aspect. There is a Duke University page describing Huffman coding that uses the phrase “go go gophers”. For lack of anything better we will use the same.
With LZ77 disabled and running only that phrase our frequency sort yields the following.
bruce_dev /> jtest flash/gogo.dat
3 0x067 3
5 0x06f 3
1 0x020 2
2 0x065 1
4 0x068 1
6 0x070 1
7 0x072 1
8 0x073 1
Processing 0.649 seconds.
Source 13 bytes.
Result 13 bytes.
Ratio 1.00:1
bruce_dev />
bruce_dev /> cat flash/gogo.dat
go go gophers
bruce_dev />We also ignore any end-of-block code.
The Duke page demonstrates that this phrase can be encoded with just 37 bits. It also demonstrates that there are multiple possible Huffman trees that can be created to yield that result. Interesting that none of them there meet the DEFLATE requirement. So I am going to determine the procedure that creates the right kind of table.
The game next is to combine pairs of leaves into nodes, And then pairs of leaves and nodes into other nodes. This procedure is repeated until there is only one at the head of the tree. Generally one is directed to combine the lowest two weighted leaves or nodes into a single node of combined weight.
Each time a node is constructed that defines a bit 0/1 for left/right for the one or two members the node contains. By working from the lowest weighted or least frequent leaves and then nodes one ends up building longer codes for that than the higher frequency values which are not touch right away.
The following procedure generates a tree (but not the kind we want just yet) using just such a procedure. The lowest two are combined and the list is resorted. We dump and repeat.
// generate tree
while (cnt > 1) {
// take lowest weight nodes and create new
int left = order[cnt - 2];
int right = order[cnt - 1];
Node nd1 = nodes.get(left);
Node nd2 = nodes.get(right);
nodes.add(new Node(left, right, nd1.weight + nd2.weight));
order[cnt - 2] = nodes.size() - 1;
cnt--;
// sort
for (int n = 0; n < cnt - 1; n++) {
nd1 = nodes.get(order[n]);
nd2 = nodes.get(order[n + 1]);
if (nd1.weight < nd2.weight) {
int k = order[n];
order[n] = order[n + 1];
order[n + 1] = k;
n -= 2;
if (n < -1)
n = -1;
}
}
//dump
System.out.println("");
for (int n = 0; n < cnt; n++) {
Node nd = nodes.get(order[n]);
if (nd.left == 0 && nd.right == 0)
System.out.printf("%d 0x%03x %d\n", order[n], nd.value, nd.weight);
else
System.out.printf("%d %d-%d %d\n", order[n], nd.left, nd.right, nd.weight);
}
}
You can follow the procedure in the output although the resulting tree is not displayed. I might create a way to display the tree but I haven’t gone that far yet.
bruce_dev /> jtest flash/gogo.dat
3 0x067 3
5 0x06f 3
1 0x020 2
2 0x065 1
4 0x068 1
6 0x070 1
7 0x072 1
8 0x073 1
3 0x067 3
5 0x06f 3
1 0x020 2
9 7-8 2
2 0x065 1
4 0x068 1
6 0x070 1
3 0x067 3
5 0x06f 3
1 0x020 2
9 7-8 2
10 4-6 2
2 0x065 1
3 0x067 3
5 0x06f 3
11 10-2 3
1 0x020 2
9 7-8 2
12 1-9 4
3 0x067 3
5 0x06f 3
11 10-2 3
13 5-11 6
12 1-9 4
3 0x067 3
14 12-3 7
13 5-11 6
15 14-13 13
Processing 0.865 seconds.
Source 13 bytes.
Result 13 bytes.
Ratio 1.00:1
bruce_dev />Here the new nodes display node reference indexes as left-right instead of a value.
Now with a tree built I create a recursive routine to walk the tree and assign leaves a code length and binary code. I then collect these leaves into a node array that would allow me to efficiently translate the raw data. Here that array is dumped. You will see the new code later. Here’s the table from the prior procedure.
0x020 ' ' count=2 length=3 code 000 0x065 'e' count=1 length=3 code 111 0x067 'g' count=3 length=2 code 01 0x068 'h' count=1 length=4 code 1100 0x06f 'o' count=3 length=2 code 10 0x070 'p' count=1 length=4 code 1101 0x072 'r' count=1 length=4 code 0010 0x073 's' count=1 length=4 code 0011
if we manually encode the phrase we see that it does in fact compress to just 37 bits.
g o ' ' g o ' ' g o p h e r s 01 10 000 01 10 000 01 10 1101 1100 111 0010 0011 total 37 bits
But this table does not meet the DEFLATE requirements and cannot fit the shorthand.
By the way here are two other tables from the Duke University page. Both of these are different yet again from our table but each gets the job done. None of these meet the DEFLATE requirement.
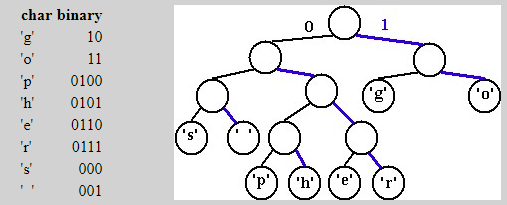
Now that third tree is close. But here is the tree that we need to learn to generate from this data.
Why? Because the two additional requirements are met.
First the code lengths (depth of the tree) increase from left to right.
Second, for the same code length (depth) the values increase from left to right (lexicographically).
And with this tree we can apply the required shorthand to properly to fit the DEFLATE format. The details of that shorthand I will get into.
Let’s revise the procedure to consider pairs of nodes from right to left.
Here we first determine the combined weight of the rightmost pair. We will combine that pair and any prior pair whose combined weight is less than or equal to that. We repeat this until we have only one node that being the head of the tree.
// generate tree
while (cnt > 1) {
// determine to combined weight of the lowest two nodes
int left = order[cnt - 2];
int right = order[cnt - 1];
Node nd1 = nodes.get(left);
Node nd2 = nodes.get(right);
int weight = nd1.weight + nd2.weight;
// Now combine node pairs equal to or less than this weight from
// right to left.
int pos = cnt;
while (pos >= 2) {
// Get the combined weight of the pair preceeding the pointer. We will
// combine the psir if its weight is less than or equal to that of
// the rightmost (least) pair. We stop if not.
left = order[pos - 2];
right = order[pos - 1];
nd1 = nodes.get(left);
nd2 = nodes.get(right);
int w = nd1.weight + nd2.weight;
if (w > weight)
break;
// Combine the pair and reduce teh order array.
nodes.add(new Node(left, right, w));
order[pos - 2] = nodes.size() - 1;
for (int n = pos; n < cnt; n++)
order[pos - 1] = order[n];
cnt--;
// onto the the next prior pair
pos -= 2;
}
//dump
System.out.println("");
for (int n = 0; n < cnt; n++) {
Node nd = nodes.get(order[n]);
if (nd.left == 0 && nd.right == 0)
System.out.printf("%d 0x%03x %d\n", order[n], nd.value, nd.weight);
else
System.out.printf("%d %d-%d %d\n", order[n], nd.left, nd.right, nd.weight);
}
}
Now when this is executed we obtain a different tree. This one actually is the one we seek.
0x020 ' ' count=2 length=3 code 100 0x065 'e' count=1 length=3 code 101 0x067 'g' count=3 length=2 code 00 0x068 'h' count=1 length=4 code 1100 0x06f 'o' count=3 length=2 code 01 0x070 'p' count=1 length=4 code 1101 0x072 'r' count=1 length=4 code 1110 0x073 's' count=1 length=4 code 1111
bruce_dev /> jtest flash/gogo.dat
3 0x067 3
5 0x06f 3
1 0x020 2
2 0x065 1
4 0x068 1
6 0x070 1
7 0x072 1
8 0x073 1
3 0x067 3
5 0x06f 3
1 0x020 2
2 0x065 1
10 4-6 2
9 7-8 2
3 0x067 3
5 0x06f 3
12 1-2 3
11 10-9 4
14 3-5 6
13 12-11 7
15 14-13 13
0x020 ' ' count=2 length=3 code 100
0x065 'e' count=1 length=3 code 101
0x067 'g' count=3 length=2 code 00
0x068 'h' count=1 length=4 code 1100
0x06f 'o' count=3 length=2 code 01
0x070 'p' count=1 length=4 code 1101
0x072 'r' count=1 length=4 code 1110
0x073 's' count=1 length=4 code 1111
Processing 0.840 seconds.
Source 13 bytes.
Result 13 bytes.
Ratio 1.00:1
bruce_dev /> I may not be ready to claim victory here but this appears to be very promising. Perhaps we should return to a more complicated situation.
Alright so we re-enable the LZ77 compression and remove much of the dump output. When we run this on jniorboot.log we get the following table.
bruce_dev /> jtest jniorboot.log
0x004 '.' count=1 length=11 code 10011110110
0x00a '.' count=9 length=6 code 110000
0x00b '.' count=13 length=6 code 110100
0x00c '.' count=4 length=8 code 10110011
0x00d '.' count=5 length=6 code 110010
0x00e '.' count=8 length=7 code 1010001
0x00f '.' count=3 length=8 code 10011101
0x010 '.' count=4 length=8 code 10111100
0x011 '.' count=8 length=7 code 1001100
0x012 '.' count=2 length=10 code 1001111000
0x013 '.' count=2 length=10 code 1001111001
0x020 ' ' count=41 length=2 code 00
0x028 '(' count=1 length=11 code 10011110111
0x029 ')' count=1 length=11 code 10110111110
0x02c ',' count=6 length=6 code 110110
0x02d '-' count=5 length=6 code 110011
0x02e '.' count=7 length=8 code 10110001
0x02f '/' count=3 length=9 code 100111110
0x030 '0' count=16 length=5 code 11111
0x031 '1' count=12 length=7 code 1011100
0x032 '2' count=12 length=7 code 1011101
0x033 '3' count=6 length=6 code 110111
0x034 '4' count=10 length=7 code 1001001
0x035 '5' count=7 length=8 code 10110100
0x036 '6' count=6 length=7 code 1001010
0x037 '7' count=4 length=8 code 10111101
0x038 '8' count=9 length=6 code 110001
0x039 '9' count=9 length=6 code 100000
0x03a ':' count=10 length=6 code 111000
0x041 'A' count=4 length=7 code 1000100
0x042 'B' count=2 length=9 code 111010000
0x043 'C' count=3 length=9 code 100111111
0x044 'D' count=1 length=11 code 10110111111
0x045 'E' count=2 length=9 code 111010001
0x046 'F' count=1 length=10 code 1110110110
0x047 'G' count=3 length=8 code 11101110
0x048 'H' count=1 length=10 code 1110110111
0x049 'I' count=3 length=8 code 11101111
0x04a 'J' count=1 length=10 code 1011111110
0x04d 'M' count=1 length=10 code 1011111111
0x04e 'N' count=4 length=7 code 1000101
0x04f 'O' count=3 length=8 code 11101010
0x050 'P' count=4 length=9 code 101101100
0x052 'R' count=3 length=8 code 11101011
0x053 'S' count=4 length=9 code 101101101
0x054 'T' count=3 length=7 code 1000110
0x055 'U' count=1 length=10 code 1110100110
0x057 'W' count=1 length=10 code 1110100111
0x05b '[' count=1 length=10 code 1110110100
0x05d ']' count=1 length=10 code 1110110101
0x061 'a' count=8 length=7 code 1001101
0x062 'b' count=5 length=7 code 1010010
0x063 'c' count=7 length=8 code 10110101
0x064 'd' count=9 length=6 code 100001
0x065 'e' count=29 length=4 code 0110
0x066 'f' count=1 length=10 code 1110100100
0x067 'g' count=2 length=10 code 1011011100
0x068 'h' count=2 length=10 code 1011011101
0x069 'i' count=14 length=6 code 101011
0x06b 'k' count=2 length=9 code 101111100
0x06c 'l' count=10 length=6 code 111001
0x06d 'm' count=6 length=7 code 1001011
0x06e 'n' count=9 length=7 code 1010000
0x06f 'o' count=17 length=4 code 0111
0x070 'p' count=5 length=7 code 1010011
0x072 'r' count=17 length=5 code 11110
0x073 's' count=11 length=7 code 1001000
0x074 't' count=15 length=6 code 101010
0x075 'u' count=8 length=8 code 10110000
0x076 'v' count=4 length=8 code 10011100
0x077 'w' count=2 length=9 code 101111101
0x079 'y' count=5 length=8 code 10110010
0x07a 'z' count=1 length=10 code 1110100101
0x100 '.' count=1 length=10 code 1011111100
0x101 '.' count=30 length=3 code 010
Processing 10.284 seconds.
Source 954 bytes.
Result 680 bytes.
Ratio 1.40:1
bruce_dev />Well okay. Just about all you can say is that it does appear that the stuff with the higher counts (frequency) does appear to use the shortest code lengths. Another good clue is the fact that the first alphabet entry that uses the smallest code is represented by a sequence of all zeroes.
I suppose now we get into what I have been calling the shorthand storage format for Huffman table. If this table can be so represented and the table reconstructed from that then we are good to go.
Huffman table “Shorthand”
While “shorthand” is my term and no one else’s that I’ve seen, it still refers to efficiently conveying the table. To start I have defined an entry for 285 possible codes each with a count and a binary code. Even with some cute integer packing this is still a lot of bytes. Having to pass the table with the compressed file painfully can cut into the benefit of the compression.
It turns out that if the Huffman table conforms to the two special rules it can be reconstructed from only knowing the code length for each of the alphabet members. So we don’t need to include the actual code.
Once we have the code lengths for each alphabet that gets packed further. It’s a bit crazy. The array of 285 code lengths contains a lot of repetition. This is packed using a form and run-length encoding where sequences of the same length are defined by the count (run length). Then that data is again (ugh) run through a Huffman encoding which results in just 19 bit lengths. Those are stored in a weird order which is intended to keep those alphabet members whose bit lengths are likely to be 0 near the end as trailing zeroes need not be included. So the entire Huffman table ends up being conveyed in just a handful of bytes. I guess people were really creative back then.
The procedure for reconstructing the Huffman table from the code lengths first requires a count of codes for each length. Let me add that to our table output. Here is the additional output from the execution.
Length=2 Count 1 Length=3 Count 1 Length=4 Count 2 Length=5 Count 2 Length=6 Count 13 Length=7 Count 15 Length=8 Count 14 Length=9 Count 8 Length=10 Count 15 Length=11 Count 4
From this table we can calculate the first binary code assigned to that code length group. Each alphabet member using that code length is then assigned an incremental binary value from that. I can add that calculation to the this table.
Length=2 Count 1 Start Code 00 Length=3 Count 1 Start Code 010 Length=4 Count 2 Start Code 0110 Length=5 Count 2 Start Code 10000 Length=6 Count 13 Start Code 100100 Length=7 Count 15 Start Code 1100010 Length=8 Count 14 Start Code 11100010 Length=9 Count 8 Start Code 111100000 Length=10 Count 15 Start Code 1111010000 Length=11 Count 4 Start Code 11110111110
Okay so I can see that the Huffman table generated DOES NOT conform. As an exercise you can see for yourself. So I wonder where error might be. Hmm…
bruce_dev /> jtest jniorboot.log
0x004 '.' count=1 length=11 code 10011110110
0x00a '.' count=9 length=6 code 110000
0x00b '.' count=13 length=6 code 110100
0x00c '.' count=4 length=8 code 10110011
0x00d '.' count=5 length=6 code 110010
0x00e '.' count=8 length=7 code 1010001
0x00f '.' count=3 length=8 code 10011101
0x010 '.' count=4 length=8 code 10111100
0x011 '.' count=8 length=7 code 1001100
0x012 '.' count=2 length=10 code 1001111000
0x013 '.' count=2 length=10 code 1001111001
0x020 ' ' count=41 length=2 code 00
0x028 '(' count=1 length=11 code 10011110111
0x029 ')' count=1 length=11 code 10110111110
0x02c ',' count=6 length=6 code 110110
0x02d '-' count=5 length=6 code 110011
0x02e '.' count=7 length=8 code 10110001
0x02f '/' count=3 length=9 code 100111110
0x030 '0' count=16 length=5 code 11111
0x031 '1' count=12 length=7 code 1011100
0x032 '2' count=12 length=7 code 1011101
0x033 '3' count=6 length=6 code 110111
0x034 '4' count=10 length=7 code 1001001
0x035 '5' count=7 length=8 code 10110100
0x036 '6' count=6 length=7 code 1001010
0x037 '7' count=4 length=8 code 10111101
0x038 '8' count=9 length=6 code 110001
0x039 '9' count=9 length=6 code 100000
0x03a ':' count=10 length=6 code 111000
0x041 'A' count=4 length=7 code 1000100
0x042 'B' count=2 length=9 code 111010000
0x043 'C' count=3 length=9 code 100111111
0x044 'D' count=1 length=11 code 10110111111
0x045 'E' count=2 length=9 code 111010001
0x046 'F' count=1 length=10 code 1110110110
0x047 'G' count=3 length=8 code 11101110
0x048 'H' count=1 length=10 code 1110110111
0x049 'I' count=3 length=8 code 11101111
0x04a 'J' count=1 length=10 code 1011111110
0x04d 'M' count=1 length=10 code 1011111111
0x04e 'N' count=4 length=7 code 1000101
0x04f 'O' count=3 length=8 code 11101010
0x050 'P' count=4 length=9 code 101101100
0x052 'R' count=3 length=8 code 11101011
0x053 'S' count=4 length=9 code 101101101
0x054 'T' count=3 length=7 code 1000110
0x055 'U' count=1 length=10 code 1110100110
0x057 'W' count=1 length=10 code 1110100111
0x05b '[' count=1 length=10 code 1110110100
0x05d ']' count=1 length=10 code 1110110101
0x061 'a' count=8 length=7 code 1001101
0x062 'b' count=5 length=7 code 1010010
0x063 'c' count=7 length=8 code 10110101
0x064 'd' count=9 length=6 code 100001
0x065 'e' count=29 length=4 code 0110
0x066 'f' count=1 length=10 code 1110100100
0x067 'g' count=2 length=10 code 1011011100
0x068 'h' count=2 length=10 code 1011011101
0x069 'i' count=14 length=6 code 101011
0x06b 'k' count=2 length=9 code 101111100
0x06c 'l' count=10 length=6 code 111001
0x06d 'm' count=6 length=7 code 1001011
0x06e 'n' count=9 length=7 code 1010000
0x06f 'o' count=17 length=4 code 0111
0x070 'p' count=5 length=7 code 1010011
0x072 'r' count=17 length=5 code 11110
0x073 's' count=11 length=7 code 1001000
0x074 't' count=15 length=6 code 101010
0x075 'u' count=8 length=8 code 10110000
0x076 'v' count=4 length=8 code 10011100
0x077 'w' count=2 length=9 code 101111101
0x079 'y' count=5 length=8 code 10110010
0x07a 'z' count=1 length=10 code 1110100101
0x100 '.' count=1 length=10 code 1011111100
0x101 '.' count=30 length=3 code 010
Length=2 Count 1 Start Code 00
Length=3 Count 1 Start Code 010
Length=4 Count 2 Start Code 0110
Length=5 Count 2 Start Code 10000
Length=6 Count 13 Start Code 100100
Length=7 Count 15 Start Code 1100010
Length=8 Count 14 Start Code 11100010
Length=9 Count 8 Start Code 111100000
Length=10 Count 15 Start Code 1111010000
Length=11 Count 4 Start Code 11110111110
Processing 10.395 seconds.
Source 954 bytes.
Result 680 bytes.
Ratio 1.40:1
bruce_dev /> Yeah I had at least one glitch but trying to generate the precise tree appropriate for the DEFLATE “shorthand” still eludes me. The search engines these days are much less effective for locating useful technical information than for finding ways to separate me from my money. It seems easier to reinvent the wheel and devise my own algorithm even though I know that a simple procedure is likely documented in numerous pages on the net.
It strikes me that all we need to do is determine the optimum bit length for each of the used alphabet members. It is almost irrelevant as to where in a tree a particular member ends up. Once we have the proper bit length a tree meeting the DEFLATE requirements can be directly created.
Perhaps the simple procedure for generating a valid Huffman tree ignoring the DEFLATE requirements can be employed and without actually building a tree structure. Note that when two leaves are combined you are simply assigning another bit to them regardless of which gets ‘0’ and which gets ‘1’. The bit length is incremented for the two leaves as it is combined into a node. In fact when you combine two nodes you need only increment the bit length (depth) for all of the members below it. So in creating a node I need only keep track of all of the leaves below it. A simple linked list suffices.
Such an implementation need not even retain intermediate nodes. You just need to maintain the node membership list. You need that so you can advance the bit count for all of the leaves below as the node is combined.
Maybe you follow me to this point or maybe not. I’ll go ahead an try an implementation.
Okay this new approach is golden! And its fast! Oh and I don’t need to build any damn tree!
static void bufflush(BufferedOutputStream outfile) throws Throwable {
// Determine frequecies by counting each occurrence of a byte value.
// Here we force the end-of-block code that we know we will use.
int[] sym_cnt = new int[286];
// sym_cnt[0x100] = 1;
for (int n = 0; n < BUFPTR; n++) {
// Get the byte value. This may be escaped with 0xff.
int ch = BUFR[n] & 0xff;
// not escaped
if (ch != 0xff)
sym_cnt[ch]++;
// escaped
else {
// Get next byte.
ch = BUFR[++n] & 0xff;
// may just be 0xff itself
if (ch == 0xff)
sym_cnt[0xff]++;
// length-distance pair
else {
// obtain balance of length and distance values
int len = (ch << 8) + (BUFR[++n] & 0xff);
int dist = ((BUFR[++n] & 0xff) << 8) + (BUFR[++n] & 0xff);
// determine length code to use (257..285)
for (int k = 0; k < blen.length; k++) {
if (len < blen[k]) {
sym_cnt[257 + k]++;
break;
}
}
// determine distance code to use (0..29)
for (int k = 0; k < bdist.length; k++) {
if (dist < bdist[k]) {
sym_cnt[k]++;
break;
}
}
}
}
}
// Create node list containing symbols in our alphabet that are found in the
// data. This will be sorted and used to assign bit lengths. Note list pointers
// are stored +1 to reserve 0 as a list terminator.
int[] nodes = new int[286];
int[] cnts = new int[286];
int nodecnt = 0;
for (int n = 0; n < 286; n++) { if (sym_cnt[n] > 0) {
nodes[nodecnt] = n + 1;
cnts[nodecnt] = sym_cnt[n];
nodecnt++;
}
}
// Determine optimal bit lengths. Here we initialize a bit length array and a
// node membership list pointer array. These will be used as we generate
// the detail required for Huffman coding.
int[] sym_len = new int[286];
int[] sym_ptr = new int[286];
// Perform Huffman optimization. This loops until we've folded all the leaves
// into a single head node.
while (nodecnt > 1) {
// The leaves are sorted by decreasing frequency (counts).
for (int n = 0; n < nodecnt - 1; n++) {
if (cnts[n] < cnts[n + 1]) { int k = nodes[n]; nodes[n] = nodes[n + 1]; nodes[n + 1] = k; k = cnts[n]; cnts[n] = cnts[n + 1]; cnts[n + 1] = k; if (n > 0)
n -= 2;
}
}
// The last two leaves/nodes have the lowest frequencies and are to
// be combined. Here we increment the bit lengths for each and
// merge leaves into a single list of node members.
int ptr = nodes[nodecnt - 2];
int add_ptr = nodes[nodecnt - 1];
while (ptr > 0) {
sym_len[ptr - 1]++;
int p = sym_ptr[ptr - 1];
if (p == 0 && add_ptr > 0) {
sym_ptr[ptr - 1] = add_ptr;
p = add_ptr;
add_ptr = 0;
}
ptr = p;
}
// Combine the last two nodes by adding their frequencies and dropping
// the last.
cnts[nodecnt - 2] += cnts[nodecnt - 1];
nodecnt--;
}
// dump nonzero bit lengths
for (int n = 0; n < 286; n++) { if (sym_len[n] > 0)
System.out.printf("0x%03x '%c' count=%d optimal bits %d\n", n,
n >= 0x20 && n < 0x7f ? n : '.', sym_cnt[n], sym_len[n]);
}
outfile.write(BUFR, 0, BUFPTR);
BUFPTR = 0;
}
Running this on the “go go gophers ” test string again with LZ77 disabled yields the desired results.
bruce_dev /> jtest flash/gogo.dat 0x020 ' ' count=2 optimal bits 3 0x065 'e' count=1 optimal bits 3 0x067 'g' count=3 optimal bits 2 0x068 'h' count=1 optimal bits 4 0x06f 'o' count=3 optimal bits 2 0x070 'p' count=1 optimal bits 4 0x072 'r' count=1 optimal bits 4 0x073 's' count=1 optimal bits 4 Processing 0.540 seconds. Source 13 bytes. Result 13 bytes. Ratio 1.00:1 bruce_dev />
Now I can use this to generate the DEFLATE compatible Huffman table.
If you multiply the frequency (count) times the bit length and add them for this example you get 37 bits which we know is the optimal for this example.
The code with comments above should be reasonably understandable. If there are any questions I can describe what is going on. But basically the routine that counts occurrences of each alphabet symbol is as it was before. Unfortunately that is complicated a bit as I have to process the length-distance pointers to determine the encoding for the tally.
Next we create a list of leaves so we can combine the two with the lowest frequency of occurrence. Here’s where we simply increment the bit lengths for node members. The leaf list distills down as it would for the traditional Huffman process.
Next I can reinstate the LZ77 compressor and run this on real data. Then we can then take the process further.
We can now use the procedure detailed in the DEFLATE specification to convert assigned bit lengths into binary codes for compression. We don’t need to build a tree.
First we tally the number of symbols in our alphabet the use each bit length.
// count the occurrence of each bit length
int[] bits = new int[19];
for (int n = 0; n < 286; n++) { if (sym_len[n] > 0)
bits[sym_len[n]]++;
}
With this we can calculate the starting binary code for each bit length. Basically for each bit length we reserve N codes and use the next as a prefix for subsequent bit lengths.
// determine starting bit code for each bit length
int[] start = new int[19];
int c = 0;
for (int n = 0; n < 19; n++) {
start[n] = c;
c = (c + bits[n]) << 1;
}
This gives us the correct first codes as we see here.
bruce_dev /> jtest flash/gogo.dat bit length 2 count 2 first code 00 bit length 3 count 2 first code 100 bit length 4 count 4 first code 1100
Now we use these starting codes in assigning the binary codes to each symbol.
// assign codes to used alphabet symbols
int[] code = new int[286];
for (int n = 0; n < 286; n++) { if (sym_len[n] > 0)
code[n] = start[sym_len[n]]++;
}
This results are displayed by the attached program.
bruce_dev /> jtest flash/gogo.dat
bit length 2 count 2 first code 00
bit length 3 count 2 first code 100
bit length 4 count 4 first code 1100
0x020 ' ' count=2 optimal bits 3 100
0x065 'e' count=1 optimal bits 3 101
0x067 'g' count=3 optimal bits 2 00
0x068 'h' count=1 optimal bits 4 1100
0x06f 'o' count=3 optimal bits 2 01
0x070 'p' count=1 optimal bits 4 1101
0x072 'r' count=1 optimal bits 4 1110
0x073 's' count=1 optimal bits 4 1111
Processing 0.654 seconds.
Source 13 bytes.
Result 13 bytes.
Ratio 1.00:1
bruce_dev />This gives us all of the codes that we need to compress our data. In this case it is for the example string “go go gophers”. Happily we did not need to build any tree structure. And, this Huffman coding is compatible with the DEFLATE specification. We can move forward with the shorthand.
Curious? Here’s what I get using jniorboot.log. The content of that file has changed by the way as I have rebooted the JNIOR during the course of this topic. Here the LZ77 compression has also been re-enabled. the program however does not yet generate the bit stream compressed with these Huffman codes.
bruce_dev /> jtest jniorboot.log
bit length 4 count 3 first code 0000
bit length 5 count 8 first code 00110
bit length 6 count 20 first code 011100
bit length 7 count 22 first code 1100000
bit length 8 count 11 first code 11101100
bit length 9 count 18 first code 111101110
0x004 '.' count=1 optimal bits 9 111101110
0x00a '.' count=8 optimal bits 6 011100
0x00b '.' count=12 optimal bits 5 00110
0x00c '.' count=5 optimal bits 7 1100000
0x00d '.' count=5 optimal bits 7 1100001
0x00e '.' count=6 optimal bits 6 011101
0x00f '.' count=3 optimal bits 8 11101100
0x010 '.' count=5 optimal bits 7 1100010
0x011 '.' count=7 optimal bits 6 011110
0x012 '.' count=4 optimal bits 7 1100011
0x013 '.' count=4 optimal bits 7 1100100
0x020 ' ' count=41 optimal bits 4 0000
0x028 '(' count=1 optimal bits 9 111101111
0x029 ')' count=1 optimal bits 9 111110000
0x02c ',' count=6 optimal bits 6 011111
0x02d '-' count=5 optimal bits 7 1100101
0x02e '.' count=7 optimal bits 6 100000
0x02f '/' count=3 optimal bits 8 11101101
0x030 '0' count=18 optimal bits 5 00111
0x031 '1' count=15 optimal bits 5 01000
0x032 '2' count=9 optimal bits 6 100001
0x033 '3' count=8 optimal bits 6 100010
0x034 '4' count=9 optimal bits 6 100011
0x035 '5' count=5 optimal bits 7 1100110
0x036 '6' count=4 optimal bits 7 1100111
0x037 '7' count=5 optimal bits 7 1101000
0x038 '8' count=7 optimal bits 6 100100
0x039 '9' count=8 optimal bits 6 100101
0x03a ':' count=9 optimal bits 6 100110
0x041 'A' count=4 optimal bits 7 1101001
0x042 'B' count=2 optimal bits 8 11101110
0x043 'C' count=2 optimal bits 8 11101111
0x044 'D' count=1 optimal bits 9 111110001
0x045 'E' count=2 optimal bits 8 11110000
0x046 'F' count=1 optimal bits 9 111110010
0x047 'G' count=3 optimal bits 7 1101010
0x048 'H' count=1 optimal bits 9 111110011
0x049 'I' count=2 optimal bits 8 11110001
0x04a 'J' count=1 optimal bits 9 111110100
0x04d 'M' count=1 optimal bits 9 111110101
0x04e 'N' count=4 optimal bits 7 1101011
0x04f 'O' count=3 optimal bits 7 1101100
0x050 'P' count=5 optimal bits 7 1101101
0x052 'R' count=3 optimal bits 7 1101110
0x053 'S' count=4 optimal bits 7 1101111
0x054 'T' count=3 optimal bits 7 1110000
0x055 'U' count=1 optimal bits 9 111110110
0x057 'W' count=1 optimal bits 9 111110111
0x05b '[' count=1 optimal bits 9 111111000
0x05d ']' count=1 optimal bits 9 111111001
0x061 'a' count=8 optimal bits 6 100111
0x062 'b' count=5 optimal bits 7 1110001
0x063 'c' count=7 optimal bits 6 101000
0x064 'd' count=9 optimal bits 6 101001
0x065 'e' count=29 optimal bits 4 0001
0x066 'f' count=1 optimal bits 9 111111010
0x067 'g' count=2 optimal bits 8 11110010
0x068 'h' count=2 optimal bits 8 11110011
0x069 'i' count=14 optimal bits 5 01001
0x06b 'k' count=2 optimal bits 8 11110100
0x06c 'l' count=10 optimal bits 6 101010
0x06d 'm' count=6 optimal bits 6 101011
0x06e 'n' count=9 optimal bits 6 101100
0x06f 'o' count=17 optimal bits 5 01010
0x070 'p' count=5 optimal bits 7 1110010
0x072 'r' count=17 optimal bits 5 01011
0x073 's' count=11 optimal bits 6 101101
0x074 't' count=15 optimal bits 5 01100
0x075 'u' count=8 optimal bits 6 101110
0x076 'v' count=4 optimal bits 7 1110011
0x077 'w' count=2 optimal bits 8 11110101
0x079 'y' count=5 optimal bits 7 1110100
0x07a 'z' count=1 optimal bits 9 111111011
0x100 '.' count=1 optimal bits 9 111111100
0x101 '.' count=28 optimal bits 4 0010
0x102 '.' count=6 optimal bits 6 101111
0x103 '.' count=2 optimal bits 8 11110110
0x105 '.' count=1 optimal bits 9 111111101
0x10d '.' count=13 optimal bits 5 01101
0x10e '.' count=4 optimal bits 7 1110101
0x10f '.' count=1 optimal bits 9 111111110
0x110 '.' count=1 optimal bits 9 111111111
Processing 9.181 seconds.
Source 954 bytes.
Result 680 bytes.
Ratio 1.40:1
bruce_dev /> With the Huffman coding for DEFLATE there is one thing that we need to worry about. We need to limit the bit length to a maximum of 15. It is not very likely to occur I suspect. But this is because the bit length list for the alphabet is run-length encoded using a procedure that can only handle bit lengths of 0 to 15. Codes of 16, 17 and 18 are used to signal certain types of repetition. This is where I got the ’19’ I use in my breadboard code to dimension the bit length arrays. That need only be ’16’ as the 3 additional are repetition codes. If the Huffman coding results in a bit length exceeding 15 I will simply have to decrease the size of the block we are encoding until we are good to go.
So now that we have the ability to reasonably compress our data using LZ77 and then to compress it further with Huffman coding, we are ready to generate the DEFLATE formatted payload. It is time to tackle the “craziness” and “shorthand” that I have referred to. We can apply the run-length encoding and the second iteration of Huffman coding that are required. We are ready to generate the DEFLATE format compressed bit stream.
JANOS has been able to process JAR/ZIP files since early in its development. This was required to meet our goal of executing Java directly from the JAR files generated by the compiler. So we have been able to decipher the DEFLATE format. I just hadn’t needed to generate it. But the advantage to this is that there is already proven code parsing the DEFLATE structure. Referring to that helps to remove any question when trying to figure out how to generate such a structure.
Rather than drop this topic now that I have the LZ77 and Huffman procedures that I need, I’ll take a moment to review the final steps. Let me see if I can clarify some of it here. For our Java breadboard to produce something usable I would not only have to complete the DEFLATE programming but also encapsulate the result in the JAR/ZIP library format. That’s more effort than I need given that I will be doing just that at the C level within the OS and I need to get to that soon.
DEFLATE Formatted Data
When file data is compressed using DEFLATE and included in a JAR/ZIP library it is represented as a bit stream. That sounds simple enough but because our micro-controller works with bytes and retrieves bytes from a file data stream we need to be concerned with bit order and byte order.
Normally bits in a byte are ordered from right to left with the least significant bit (the first in the bit stream) on the right. Like this:
+--------+ |76543210| +--------+
The 9th bit in the stream then comes from the next byte and bytes are in sequence in increasing memory addresses (or increasing file position). This order of bits seems only natural as it should.
So if we were to retrieve a 5-bit value from the stream we would obtain the right 5 bits from the first byte using the mask 0x1f. Placing that in a byte of its own would give us the numeric value of the 5-bit data element. The next 5-bit element would use the remaining 3 bits in the first byte and 2 from the right side of the next. We would likely be using a right shift before applying the mask to pull those together.
Huffman codes will seem to contradict this. These codes are packed starting with the most-significant bit of the code. In other words the most significant bit of the first Huffman code would be found in the rightmost bit of the first byte. Once you realize that you must process Huffman codes a bit at a time and that you are reading single bit data elements this order makes sense. Pointing out that the Huffman code appears in the byte in reverse order serves to confuse us. But you are reading it a single bit at a time using each bit to decide which direction to descend through the Huffman tree. That means that you need the code’s most-significant bit first. We also never know in advance how many bits we are going to need to reach the first leaf of the tree and thus our first encoded member of the alphabet.
Block Format
The DEFLATE bit stream is broken down into a series of 1 or more blocks of bits. In our case when we flush our 64KB LZ77 data buffer we are going to construct a single block. Since we are compressing it you would expect that it will contain much less than 512Kb (64KB x 8 bits). For large file we will likely need to flush our buffer multiple times creating a stream with multiple blocks.
Each block contains a 3-bit header. The first bit is called BFINAL and it is a 1 only for the last block in the stream. The next 2 bits are called BTYPE and these define the data encoding for this block. That means that we could use a different encoding for each block if we felt it to be beneficial. The 2 BTYPE bits gives us 4 options.
00 - no compression 01 - compressed with fixed Huffman codes 10 - compressed with dynamic Huffman codes 11 - reserved (error)
We have been working toward being able to generate blocks of BTYPE 10. We could have used the predefined Huffman tables in BTYPE 01 or not even bothered to compress using BTYPE 00. There may be times when our compression fails to reduce the size of our file data. IN that case we could decide to include a block without compressing. But for now we will concern ourselves with BTYPE 10 that includes dynamic (not adaptive) Huffman tables (tables that change block to block).
So to start this defines our block so far. I’ll show the stream progressing from left to right with the number of bits for each element shown in parentheses.
Bit 0 1 2 3 4 5 6 7 +---------+---------+---------+---------+---------+---------+---------+--------- | BFINAL | BTYPE (2) | Balance of Block . . . +---------+---------+---------+---------+---------+---------+---------+--------- BFINAL set on the last block in the stream.
Now logically we know that somehow we need to get the Huffman table before we see compressed data so we can decompress that data. We also have seen that the Huffman table can be defined knowing the bit lengths for each of the symbols in our alphabet. In fact we expect that, since I made a big deal about having the right kind of Huffman table for DEFLATE that can be generated from just the bit lengths. So we are looking for that array of bit lengths. Here’s where the fun begins.
To start we know that not all of the 286 members of the alphabet will be used in the data. Some entries in that table will be assigned a 0 bit length. We have to assume that the majority of the literal bytes (0..255) will be represented in the data. We also know that the end-of-block code (257) will appear once. So we need an array of bit lengths at least 257 entries long. Beyond that we don’t know how many of the sequence length codes (257..285) will be used. But if some of the trailing codes aren’t used then the array doesn’t need to be 286 entries long. We just need the non-zero bit lengths. So this array will be 257 plus however many length codes we need to cover all of the non-zero ones.
The next element in the bit stream is HLIT. This is a 5-bit element when added to 257 defines the count of entries in the bit length array that will be provided. We will assume that the reset are 0. Since there are 29 length codes beyond the end-of-block code we need only know how many of those to know the size of the array. That can be passed in a 5-bit element.
Bit 0 1 2 3 4 5 6 7
+---------+---------+---------+---------+---------+---------+---------+---------+-----
| BFINAL | BTYPE (2) | HLIT (5) |
+---------+---------+---------+---------+---------+---------+---------+---------+-----
HLIT + 257 tells us how many of the 286 bit lengths will be provided. But, don’t expect that those will be forthcoming. At least not right away.
Next comes something that the breadboard program handled incorrectly. The distance codes for the length-distance pointers are Huffman coded using their own table. The length codes are Huffman coded using the same table as the literal data. This makes sense since when you retrieve the next code you don’t know if it is a literal or a length code. You do know that after the length code (and any extra bits) comes the distance code. So compressing those with their own table is a benefit. The DEFLATE specification (RFC 1951) states this but it isn’t all that obvious.
So wait! Now we need 2 Huffman tables and therefore 2 arrays of bit lengths. Yes we do.
Next we receive a 5-bit data element containing HDIST – 1. This defines the number of bit lengths to be supplied for the distance alphabet and the second Huffman table. The specification shows that there are 30 distance codes (0..29) but refers to 32 distance codes. It states that codes 30 and 31 will never occur in the data. These are perhaps reserved to allow for a larger sliding window in the future. There is also the need for a 0 distance code which would be used as a flag to indicate that no distance codes are used at all and that the data is all literals. So to pass a bit length array size of up to 33 the value is stored -1.
Bit 0 1 2 3 4 5 6 7
+---------+---------+---------+---------+---------+---------+---------+---------+-----
| BFINAL | BTYPE (2) | HLIT (5) |
+---------+---------+---------+---------+---------+---------+---------+---------+-----
8 9 10 11 12 13 14 15
-----+---------+---------+---------+---------+---------+---------+---------+---------+-----
| HDIST (5) |
-----+---------+---------+---------+---------+---------+---------+---------+---------+-----
Now we know the length of two arrays defining bit lengths for two alphabets. I had alluded to the fact that we would again use Huffman coding to compress the bit length array data. That is the case and so we need yet another Huffman table and therefore a third array of bit lengths. Will it never end??
The bit length alphabet includes 3 codes for repetition for total of 19 codes. The size of the bit length array for this is conveyed in a 4-bit data element HCLEN – 4. Note though that this array defines bit lengths for the codes in a very specific order. This was devised to keep those codes that typically have 0 bit length at the end of the array so they can be omitted. The order of the codes is as follows:
16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15
That means that we will have to arrange the bit lengths in this order before deciding how many to include in our stream. When reading these we would shuffle them into the proper location.
Our bit stream now looks like this.
Bit 0 1 2 3 4 5 6 7
+---------+---------+---------+---------+---------+---------+---------+---------+-----
| BFINAL | BTYPE (2) | HLIT (5) |
+---------+---------+---------+---------+---------+---------+---------+---------+-----
8 9 10 11 12
-----+---------+---------+---------+---------+---------+-----
| HDIST (5) |
-----+---------+---------+---------+---------+---------+-----
13 14 15 16
-----+---------+---------+---------+---------+-----
| HCLEN (4) |
-----+---------+---------+---------+---------+-----
Well there is a lot of information so far conveyed in just 2 bytes. Next we will finally receive some bit length data. Following this we are supplied HCLEN + 4 data elements each 3-bits (0..15) defining the code lengths for the Huffman table that we will use to generate bit length arrays for the other tables. Note that these are in the predefined order and must be sorted into the bit lengths for the 19 symbol alphabet. Now there are a variable number of these data elements and so I will no longer be able to number the bits nor can I show them all. HCLEN + 4 data elements however many is required follow in the stream.
13 14 15 16 17 18 19 . . .
-----+---------+---------+---------+---------+---------+---------+---------+-----
| HCLEN (4) | CODE16 (3) |
-----+---------+---------+---------+---------+---------+---------+---------+-----
-----+---------+---------+---------+---------+---------+---------+-----
| CODE17 (3) | CODE18 (3) |
-----+---------+---------+---------+---------+---------+---------+-----
-----+---------+---------+---------+---------+-----
| CODE0 (3) | . . .
-----+---------+---------+---------+---------+-----
We now have a bit length array for our 19 symbol alphabet. At least we are familiar with this from the breadboard program. We can use the procedure to generate the Huffman code table. First we count the number of times each bit length is used. Then we calculate a starting code for each length. And then we assign sequential codes to the alphabet for each bit length group. So we can decipher Huffman codes. It’s a good thing too because now what follows in the bit stream are Huffman codes from this table.
Keeping up? We are talking about what is involved in decompressing a DEFLATE stream but really we are doing this so we know what to do when we compress our own data. So now is the time to consider dropping some bread crumbs because if you are going to create a DEFLATE stream you will need to find your way back through this.
Supposedly at this point we can read Huffman codes, locate the symbol they represent and retrieve the bit length array data we were originally looking for. Well almost. While some of the values we obtain will be bit lengths for the next entry in a bit length array there are 3 special codes each requiring a different action. The specification describe them as follows.
0 - 15: Represent code lengths of 0 - 15
16: Copy the previous code length 3 - 6 times.
The next 2 bits indicate repeat length
(0 = 3, ... , 3 = 6)
Example: Codes 8, 16 (+2 bits 11),
16 (+2 bits 10) will expand to
12 code lengths of 8 (1 + 6 + 5)
17: Repeat a code length of 0 for 3 - 10 times.
(3 bits of length)
18: Repeat a code length of 0 for 11 - 138 times
(7 bits of length)
Here we see that when we encounter one of the codes 16, 17 or 18 we are required to pull 2, 3 or 7 additional bits respectively from the bit stream which define a repeat count.
First we will receive Huffman codes to define HLIT + 257 bit lengths for the literal Huffman table. Then we will receive codes defining HDIST + 1 bit lengths for the distance Huffman table. But don’t think the fun ends here.
HLIT and HDIST do not define the count of Huffman codes that follow. If you obtain a code that repeats a value that counts for that many bit lengths. That perhaps makes sense. But to just make things a little trickier, once you acquire the HLIT + 257 codes you immediately start defining the HDIST + 1 codes even if you are performing repetition. Yeah, a single repeat code can take you from one table to the next. If you are repeating some 0 bit lengths trailing in the HLIT bit length array you would just keep going to define any 0 bit lengths in the first part of the HDIST array. The specification says “code lengths form a single sequence of HLIT + HDIST + 258 values.”
When you are generating these Huffman codes of course you don’t have to force it to be a single sequence. You might just be wasting a few bits. Today that’s not a big deal but it certainly must have been 40 years ago.
So start pulling Huffman codes. Remember you process these 1 bit at a time so you are starting with the most-significant bit of some code. With each bit you are either descending through a tree looking for a leaf and the corresponding symbol or otherwise collecting the code looking for a match in a code list. The former is faster but the latter easier to structure in memory (no tree). You proceed to process each symbol to define a bit length or repetition code.
Now you have 2 tables of bit lengths and you know how to generate the Huffman codes for the associated alphabets. What follows next in our bit stream are the actual Huffman codes for the compressed data block. Each Huffman code will either define a literal value (byte) or a length code. The byte you just push into your uncompressed stream and the sliding window. In the case of a length code you would retrieve the additional bits defining the length of a matched sequence. You would then use the distance Huffman table for the next code that together with extra bits defines a distance back into the sliding window. Push the referenced string into your uncompressed stream and the sliding window. This is repeated until you encounter the end-of-block code (256). If BFINAL was set for the block you can save your now uncompressed data and you are done. Otherwise another block will follow.
Now we follow this logic backwards to figure out for our own compression effort what we need to do to generate the proper DEFLATE format for our data.
Okay, feel free to post questions, comments, corrections or whatever. I would be curious to know if I have helped anyone. I have written these posts as a form of review and preparation for myself. I am now ready to generate some C code in JANOS to make perhaps broad use of DEFLATE.
- This will allow the existing JAR/ZIP JANOS command to create or modify compressed file collections. That will be helpful in applications that generate massive amounts of log data.
- It will let JANOS create PNG graphics using drawing and plotting commands. This will allow us to easily display the data acquired by monitoring applications.
- The WebServer can utilize DEFLATE to more efficiently transfer content. It can really help here as we already serve files (the DCP for example) directly out of a ZIP library. Whereas we presently decompress those files and send uncompressed content, the WebServer could forward the DEFLATE formatted data directly providing a bandwidth benefit.
The JANOS WebServer uniquely can locate and serve content directly from ZIP file collections. Generally files in a ZIP collection are compressed in DEFLATE format already. The WebServer can detect a browser’s ability to accept content in DEFLATE format directly and transfer the compressed content directly. Why spend the time to decompress before transfer?
Since this does not involve a DEFLATE compressor it was quick to implement. Starting with JANOS v1.6.4 (now in Beta) the WebServer will utilize DEFLATE content encoding when transferring files already compressed in that format provided that the browser can accept it. It works nicely.
I’ve been busy extending the JAR/ZIP command in JANOS to allow you to create, update and freshen an archive file. The first step was to just store files uncompressed. Getting all of that command line logic straight is enough of a headache. Once that was behind me I was ready to implement DEFLATE.
One difference in the JANOS implementation from the approach taken earlier in this thread is that I am going to work with buffers as opposed to a byte stream. Since the JNIOR uses a 64MB heap and generally consumes only a few MB of it I can load an entire file’s content in a memory buffer. Yeah, files on the JNIOR aren’t very large. This eliminates the queue approach to the sliding window. That helps with matching as it eliminates any need to test pointers for wrap around.
Where I used a bidirectional linked list before tracking occurrences of each byte value in the sliding window, I have gravitated to a series of queues tracking the last 256 matching bytes (or fewer if that be the case) in the 32KB preceding window. There is also no need now to keep any array of active matches since we are not streaming. So a pass through the appropriate queue for the current byte generally delivers a usable match and limits the search times in interest of speed. I get results within 2% or so of what the PC generates for the same file. This is certainly acceptable for JANOS.
I use the code length generator algorithm that I devised previously so as to not have to generate any Huffman tree physically. This for certain test files tended to hit the DEFLATE maximum code length limits. So I will describe a variation that seems to avoid that problem.
I will go through the implementation details here over the next day or so and maybe share some of the code. Remember that I am writing in C so…
DEFLATE Compressor Implementation (C Language)
The goal is to compress using DEFLATE a byte buffer filled with the entire contents of a file or other data. I want a simple function call like this:
FZIP_deflate(fbuff, filesize, &cbuff, &csize)
This function needs to return two things, a buffer containing the DEFLATE formatted bit stream and the compressed length. There are other ways to return these parameters but for JANOS which has to remain thread-safe (cannot use static variables) this works. This routine returns TRUE if we can successfully compress the data. It might return FALSE if in compressing the results we decide it isn’t going to be worth it. This function is used as follows in the JAR/ZIP command in JANOS.
// optionally compress
compressed = FALSE;
compsize = filesize;
if (filesize >= 128)
{
char *cbuff = NULL;
uint32_t csize;
// compress the content
if (FZIP_deflate(fbuff, filesize, &cbuff, &csize))
{
compressed = TRUE;
compsize = csize;
MM_free(fbuff);
fbuff = cbuff;
}
else
MM_free(cbuff);
}
Here we see that successful compression replaces the uncompressed buffer and modifies the compressed data size. It sets the compressedflag so the file can be properly saved in the JAR or ZIP archive. Like magic we have a compressed file!
Preface
Why am I doing this? I mean there is code out there and people have been able to construct archives and compress files literally for multiple decades. Why reinvent the wheel?
Well there are multiple reasons. First is a design goal for JANOS. This operating system uses no third-party written code. That sounds crazy but what it means is that there is no bug or performance that we cannot correct, change, improve or alter. And, this can be done quickly and in a timely fashion. Every bit of code is understood, clearly written and documented. It is written for a single target and not littered with conditional compilation blocks which obfuscate everything. If you support an operating system you might see how you could be envious of this.
Another reason is educational. Now that maybe is selfish but if I am going to be able to fully debug something I need to fully understand it. We cannot tolerate making what seems like a simple bug correction which later turns out to break some other part of the system. The only way to guarantee that this risk is minimized is for me to know everything that is going on and exactly what is going on. Yeah there is a JVM in here. Yeah it does TLS v1.2 encryption. It’s been fun.
The real problem though is that it is difficult to find good and complete technical information on the net. Yes there is RFC 1951 defining DEFLATE. It does not tell how to do it just tells you what you need to do. And, some aspects of it are not clear until you encounter it (or recreate it) in action. It describes LZ77 but you don’t realize that this is very difficult to implement and not have it take 5 minutes to compress 100 KB.
There are numerous web pages discussing DEFLATE and some by reputable universities. These usually include a good discussion on Huffman coding. Yet I have found none the creates a Huffman table that actually meets the additional requirements for DEFLATE. If you are going to describe Huffman in connection with DEFLATE, shouldn’t it be compatible? Would it have helped if you actually had implemented DEFLATE before describing it?
The procedure to create a compatible Huffman tree is not described anywhere that I have found, Most don’t even mention that you need 3 separate Huffman tables (one for literals, one for distance codes and one for code lengths) and that there is a limit of a 15 bit code length for 2 of the tables and 7 bit for the third. Then they say only to “adjust the Huffman table” accordingly. So there is no procedure for generating a less than optimum Huffman tree meeting DEFLATE restrictions. I had to get creative myself.
Enough of my rant. The result really is that I have had to reinvent the wheel. I am not the only one to have done so. I am going to try to document it here for your edification.
Overview
First let me greatly over-simplify the process and provide an outline for the compression procedure.
- Perform efficient LZ77 scanning the uncompressed data byte-by-byte filling a 64 KB interim buffer with raw unmatched literal bytes and escaped length-distance references.
- Scan the interim LZ77 data creating two DEFLATE compatible Huffman tables, one for literals and length codes combined and one for distance codes.
- Assign code lengths (15 bits max) to the used alphabet for both tables.
- Determine the size of the alphabet required for the length and distance Huffman tables.
- Combine code lengths into a single run-length compressed array.
- Determine the DELFATE compatible Huffman table needed to code this compressed code length array.
- Assign code lengths (7 bits max) to the used alphabet for code lengths.
- Sort the resulting code lengths for this 3rd Huffman table into the unique order specified for DEFLATE and determine the length of the array (trim trailing zeroes),
- Output the block header marking only the last as BFINAL and output the alphabet sizes.
- Output the reordered code lengths.
- Output the Huffman codes compressing the run-length encoded combined code length array. Insert extra bits where required.
- Output the Huffman codes compressing the LZ77 data. Use the literal table for literals and sequence lengths. Use the distance table for distance codes. Insert extra bits where required.
- Output end-of-block code.
- If not the final block keep the bit stream going and continue LZ77 at step #1.
Uh. That about summarizes it. All we can do is to push through this step by step. It amounts the two phases. The first compresses the data using LZ77 and determines the Huffman coding requirements. The second outputs a bit stream encoding the Huffman tables and then the actual data. We first determine everything that we need for the bit stream and then generate the bit stream itself.
Time-Efficient LZ77 Compression
First off let me note that we end up trading off compression ratio for processing speed. As we had experimented earlier in Java we could discover every possible matching sequence for a block of data and then analyze those matches selecting the optimum set. This arguably would create the best compression possible. This is certainly doable if we are running on a multiple core GHz processor and it is coded carefully. Still it would be lengthy and possibly not appropriate even then for some applications. The gain in compression ratio is expected to be only slight and not worth the processing cycles. It is certainly not critical for JANOS. So we will not go down this path.
Another approach is what is called lazy matching. Here we are concerned that a matched sequence might prevent a longer matching sequence starting in the next byte or two from being used. In the analysis it appears that 1 or 2 bytes may be unnecessarily forced into the output stream in these situations. Those may be rare but for certain types of data it could be more of a concern. Again the gain in compression ratio if we were to take the time to perform lazy matching is assumed not to be necessary for JNIOR.
As a result we are just going to go ahead and perform straight up sequence match detection for each byte position in the data. Even with this the amount of processing involved prevents us from using any kind of brute force scanning. Imagine how much processing would be involved if for each byte in the file we have to compare it directly against 32 KB of bytes in the preceding sliding window. For a large file this is starts to become a very large number of processor cycles. It gets even worse when bytes match and you need to check following bytes to determine the usability of the sequence.
I had implemented the brute force search with no trickery at first. Small files produced proper LZ77 output in a short time but a 20 KB JSON file took almost 30 seconds (JNIOR remember). A large binary file basically stalled the system. The JSON performed more poorly due to the high occurrence of certain characters such as curly braces, quotes and colons. That code has long been discarded or I would include it here for better understanding.
In the prior Java experimentation I used a linked list to track the occurrences of matching byte values. This eliminated the need to scan the entire 32 KB sliding window saving time. For the JANOS implementation I decided to use a pointer queue for each byte value. Each queue holding a maximum of 256 pointers. So basically we would test only the last 256 matching byte positions for usable sequences. This might miss some good sequence matches deep in the sliding window for very frequently occurring byte values but not for those appearing less often. Again it’s a trade off. It is an interesting approach.
I had figured that I could adjust the depth of these pointer queues. Since there are 256 possible literal values and each with 256 pointers which require 4 bytes this results in a matrix of 65,536 pointers or 256 KB of memory. There is room for that in the JANOS heap. Increasing the depth increases the memory requirement as well as the time spent in sequence detection. I was pleased with the results at a depth of 256. Perhaps later I will conduct some experiments plotting the effects of this parameter on compression ration and execution time.
I will present the resulting routine in the next post.
Here is the resulting routine. This handles only the LZ77 leaving all of the Huffman to the routine responsible for flushing the interim buffer. Note that I have made both the SLIDING_WINDOW and DEPTH parameters adjustable through the Registry. I will use this later to measure performance.
/* -- function ---------------------------------------------------------------
** FZIP_deflate()
**
** Compresses the supplied buffer.
**
** -------------------------------------------------------------------------*/
int FZIP_deflate(char *inb, uint32_t insize, char **outbuf, uint32_t *outsize)
{
char *obuf;
int optr;
int err = FALSE;
int curptr, len, seqlen;
char *seqptr, *p1, *p2, *s1, *s2;
struct bitstream_t stream;
int *matrix, *mat, *track;
int ch, trk;
int window, depth;
// obtain sliding window size
window = REG_getRegistryInteger("Zip/Window", 16384);
if (window < 2048) window = 2048; else if (window > 32768)
window = 32768;
// obtain tracking queue depth
depth = REG_getRegistryInteger("Zip/Depth", 256);
if (depth < 16) depth = 16; else if (depth > 1024)
depth = 1024;
// check call
if (outbuf == NULL || outsize == NULL)
return (FALSE);
// initialize bit stream
memset(&stream, 0, sizeof(struct bitstream_t));
stream.buffer = MM_alloc(insize + 1024, &_bufflush);
// create an output buffer
obuf = MM_alloc(64 * 1024, &FZIP_deflate);
optr = 0;
// initialize matrix
matrix = MM_alloc(256 * depth * sizeof(int), &FZIP_deflate);
track = MM_alloc(256 * sizeof(int), &FZIP_deflate);
// process uncompressed stream byte-by-byte
curptr = 0;
while (curptr < insize)
{
// get current byte value
ch = inb[curptr];
// Locate best match. This is the longest match located the closest to the curPtr. This
// is intended to be fast at the slight cost in compression ratio. We do not handle lazy
// matches or block optimization (selective matching). Only seqlen of 3 or more matter so
// we initialize seqlen to 2 to limit unnecessary best match updates. Try to limit cycles in
// this loop.
mat = &matrix[depth * ch];
trk = track[ch] - 1;
if (trk < 0) trk = depth - 1; seqlen = 2; p2 = &inb[curptr]; while (trk != track[ch]) { if (mat[trk] == 0 || curptr - mat[trk] >= window)
break;
s1 = p1 = &inb[mat[trk] - 1];
s2 = p2;
while (*s1 == *s2)
s1++, s2++;
// check for improved match
len = s1 - p1;
if (len > seqlen)
{
seqptr = p1;
seqlen = len;
}
trk--;
if (trk < 0) trk = depth - 1; } // track the character mat[track[ch]] = curptr + 1; track[ch]++; if (track[ch] >= depth)
track[ch] = 0;
// check validity (match past end of buffer)
if (curptr + seqlen > insize)
seqlen = insize - curptr;
// If we have a good sequence we output a pointer and advance curPtr
if (seqlen >= 3)
{
// check maximum allowable sequence which is 258 bytes but we reserve one
// for 0xff escaping
if (seqlen > 257)
seqlen = 257;
// escape length-distance pointer
obuf[optr++] = 0xff;
obuf[optr++] = seqlen - 3;
*(short *)&obuf[optr] = p2 - seqptr;
optr += 2;
// advance curPtr
curptr += seqlen;
PROC_yield();
}
// otherwise we output the raw uncompressed byte and keep searching
else
{
// escape 0xff
if (*p2 == 0xff)
obuf[optr++] = 0xff;
obuf[optr++] = *p2;
curptr++;
}
// flush output buffer as needed. Because we escape 0xff our length-pointer encoding
// requires 4 bytes. This at times replaces a 3-byte match and so the compression
// ration in this buffer is compromised. That will be corrected as we move into
// Huffman coding. Blocks will then be slightly less than 64KB. We also want to
// flush this before over-running it.
if (optr > 65530)
{
if (!_bufflush(obuf, optr, &stream, FALSE))
err = TRUE;
// if compression seems fruitless
if (stream.length > curptr)
err = TRUE;
optr = 0;
}
if (err)
break;
}
// Flush remaining data
if (!err && !_bufflush(obuf, optr, &stream, TRUE))
err = TRUE;
// if compression was fruitless
if (stream.length > insize)
err = TRUE;
// clean up
MM_free(track);
MM_free(matrix);
// return
*outbuf = stream.buffer;
*outsize = stream.length;
return (!err);
}
So the preliminaries are over by line 50 in this code. You might notice that when JANOS allocates memory it retains a reference pointer. That is used to locate memory leaks among other things. I can see quickly where any block is allocated.
The main loop which processes byte-by-byte through the uncompressed data is done by line 150. After that we merely flush any partially compressed block and be done.
From lines 55 to 95 we search for the best match. From 95 to about 130 we either output the sequence length-distance reference or the raw unmatched data byte. After that we check to see if we need to flush the interim buffer.
The magic occurs in the search where we employ the pointer matrix. The trk array keeps a list of current positions in the each byte value queue. This is where we add the pointer to the current byte once we’ve searched it. The search runs backward through the queue either until we’ve check all of the pointers (wraps back to the starting position) or we run out of the sliding window (pointer reference too far back in the data). This checks for closer matches first. When a longer sequence of characters matches the current position we update our best match.
After that if we have a sequence of 3 or more bytes we output the length-distance reference otherwise we output the current byte and move on to process the next.
I know that I can optimize this some more. I haven’t gone through that step of trying to minimize processor cycles. We do use the RX compiler optimization. But… this is my approach for LZ77. There is no hash table or confusing prefix-suffix tricks. It seems to run fast enough at least for our needs at this point. The LZ77 search is where all of the time is consumed.
Next we will look at what happens when the interim buffer is flushed.
The FZIP_deflate() routine involves 90+ percent of the processing time and handles only step #1 in the prior outline. The buffer flush routine handles all of the remaining items.
We will be creating three different Huffman tables. These amount to a structure for each alphabet symbol.
struct huff_t {
uint16_t code;
uint16_t len;
uint16_t cnt;
uint16_t link;
};
Here the cnt will represent the symbol’s frequency. It is the count of occurrences of the symbol’s value in the data. The len will eventually be the code length in bits assigned to the symbol. The code will hold the bit pattern to be used in coding. And the link will be used in the code length determination routine.
The _bufflush() routine is called with a buffer of LZ77 compressed data. This includes raw data bytes that could not be included in a sequence and length-distance references for matches. Since data can take on all byte values I use a form of escaping. The escape character is 0xFF and a 0xFF in the data is represented by repeating the escape (e.g. 0xff 0xff). Otherwise the next byte is the length of the sequence -3 and the following short value the distance. To make this work I disallow the sequence length of 258 since that would be confused with an escaped 0xFF. I don’t see this as having any significant impact. Later I could find a way around that but for now it works.
// Routine applies DEFLATE style Huffman coding to the buffer content.
static int _bufflush(char *obuf, int osize, struct bitstream_t *stream, int final)
{
struct huff_t *littbl;
struct huff_t *dsttbl;
struct huff_t *cnttbl;
int n, len, c, code, dst, lastc, ncnt;
int *cntlist, *litcnts, *dstcnts, *bitcnts, *bitlens;
int hlit, hdist, hclen;
int *startcd;
int totdist = 0;
int err = FALSE;
// Now we need to construct two Huffman trees (although I am going to avoid
// actual trees). One for the literal data and one for the distance codes.
// Note that extra bits are just extra bits inserted in the stream.
littbl = MM_alloc(286 * sizeof(struct huff_t), &_bufflush);
dsttbl = MM_alloc(30 * sizeof(struct huff_t), &_bufflush);
// Not a loop. This allows the use of break.
for (;;)
{
// Now we analyze the data to determine frequencies. Note that this is complicated
// just a bit because of the escaping that I have had to use. I will have to
// temporarily decode length and distance encoding. We'll have to do that again
// later when we stream the coding. We will also use one end-of-block code so we
// virtually count it first.
littbl[256].cnt = 1;
for (n = 0; n < osize; n++)
{
// tally literal if not escaped
if (obuf[n] != 0xff)
littbl[obuf[n]].cnt++;
else
{
// check and tally escaped 0xff
if (obuf[++n] == 0xff)
littbl[0xff].cnt++;
else
{
totdist++;
// table defined above
//static const int lcode_ofs[29] = {
// 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 15, 17, 19, 23, 27, 31,
// 35, 43, 51, 59, 67, 83, 99, 115, 131, 163, 195, 227, 258
//};
// determine required length code for lengths (3..258). This code is
// coded in the literal table.
len = (obuf[n++] & 0xff) + 3;
for (c = 0; c < 29; c++) if (lcode_ofs[c] > len)
break;
code = 256 + c;
littbl[code].cnt++;
// table define above
//static const int dcode_ofs[30] = {
// 1, 2, 3, 4, 5, 7, 9, 13, 17, 25, 33, 49, 65, 97, 129, 193,
// 257, 385, 513, 769, 1025, 1537, 2049, 3073, 4097, 6145,
// 8193, 12289, 16385, 24577
//};
// determine required distance code for distances (1..32768). This code is
// coded in the distance table.
dst = (obuf[n++] & 0xff) << 8;
dst |= (obuf[n] & 0xff);
for (c = 0; c < 30; c++) if (dcode_ofs[c] > dst)
break;
code = c - 1;
dsttbl[code].cnt++;
}
}
}
So here we create two of the Huffman tables, one for the literal alphabet (0..285) and one for the distance alphabet (0..29). Note that when JANOS allocates memory it is zero filled.
Don’t be confused by my use of for(;;) { }. This is not an infinite loop. In fact it is not a loop at all. Rather it allows me to exit the procedure at any point using break; and I just have to remember to place a break; at the very end. There are other ways to achieve the same thing.
The first step is to determine the frequency of symbols from both alphabets. Here we scan the supplied data and count the literals. The escaped length-distance references are translated temporarily into their length codes and distance codes. Those are tallied in the appropriate table. The extra bits are ignored. Length codes are combined with literal data since when they are read you don’t know which it will be. The distance codes use their own alphabet. We will have to do this same translation again later when we encode the references for output. Then, of course, we will insert the required extra bits.
Note that this also tallies one end-of-block code (0x100) as we will be using that.
If I were to dump these two tables after this they may look something like this. These are just the symbols that occur in a particular set of data – the jniorsys.log file. This is the symbol value followed by its count.
0x00a 2
0x00d 2
0x020 70
0x027 4
0x028 11
0x029 2
0x02a 2
0x02b 7
0x02c 7
0x02d 20
0x02e 133
0x02f 16
0x030 105
0x031 153
0x032 124
0x033 124
0x034 103
0x035 110
0x036 97
0x037 90
0x038 93
0x039 84
0x03a 74
0x03c 1
0x03d 3
0x03e 3
0x041 5
0x043 4
0x044 1
0x046 1
0x048 1
0x04a 3
0x04c 2
0x04d 4
0x04e 4
0x04f 4
0x050 8
0x052 8
0x053 4
0x054 4
0x055 1
0x057 3
0x05a 1
0x05f 3
0x061 34
0x062 4
0x063 15
0x064 26
0x065 37
0x066 9
0x067 9
0x068 8
0x069 36
0x06a 6
0x06b 3
0x06c 21
0x06d 13
0x06e 36
0x06f 41
0x070 24
0x071 1
0x072 29
0x073 20
0x074 29
0x075 11
0x076 6
0x077 7
0x078 3
0x079 6
0x07a 4
0x100 1
0x101 962
0x102 457
0x103 136
0x104 127
0x105 55
0x106 71
0x107 47
0x108 14
0x109 67
0x10a 208
0x10b 103
0x10c 40
0x10d 52
0x10e 44
0x10f 15
0x110 42
0x111 180
0x112 287
0x113 30
0x114 5
0x115 12
0x116 6
0x002 1
0x003 2
0x008 2
0x009 2
0x00a 13
0x00b 150
0x00c 166
0x00d 40
0x00e 127
0x00f 63
0x010 157
0x011 112
0x012 155
0x013 116
0x014 198
0x015 169
0x016 240
0x017 197
0x018 288
0x019 215
0x01a 321
0x01b 226We need to assign code lengths to these alphabet symbols. Here there are two tables and later we will process a third. So the procedure is handled by a separate rom.buffer;
*outsize = stream.length;
return (!err);
}
The _bitlength() routine assigns code lengths creating possibly a slightly less than optimal Huffman table that does not exceed a 15-bit maximum. The assignments must make the Huffman tables compatible with the DEFLATE requirements.
Huffman Tables for DEFLATE
The buffer full of data that we have and which has been compressed using LZ77 will be compressed further using Huffman coding. The DEFLATE format specifies two separate Huffman code sets. One to encode both the literal bytes in the data (0..255), the end-of-block code (256), and the sequence match length codes (257..285). The second Huffman code set will encode the distance codes (0..29). We can use a separate table for that because we know when we are reading a distance code as one always follows a length code. We never know whether we are reading a literal or a length code so those need to be decoded the same way and therefore from the same table.
Previously we scanned the data and counted the occurrences of each symbol. We now know which symbols occur in the data and how frequently. We have defined our alphabets for each Huffman table. Now we need to create the Huffman trees themselves. This is where things get tricky.
Creating a Huffman tree is not very difficult. But creating a Huffman tree that is compatible with the DEFLATE format is quite another thing altogether. The DEFLATE specification dictates that the Huffman trees must meet two additional rules. In fact they need to adhere to three rules. The third is mentioned later in the specification.
- All codes of a given bit length have lexicographically consecutive values, in the same order as the symbols they represent.
- Shorter codes lexicographically precede longer codes.
- The bit length cannot exceed 15 bits for the literal and distance code sets. It cannot exceed 7 bits for the code length set (comes into play much later).
The first trick is to not generate a tree at all. If you create a tree using the standard Huffman approach you are almost guaranteed to not have a tree that is usable for DEFLATE. All you need from that effort are the bit lengths that end up being assigned to each symbol. You can get those from the same procedure without dealing with right and left links and an actual tree structure. You then use the procedure defined in the DEFLATE specification to create the compatible tree.
The standard Huffman approach is to take a list of all the symbols that occur in the data and sort it in descending frequency. Combine the rightmost two least frequent symbols into a node whose frequency is the total of the two symbols. Next resort the list so this new node repositions itself according to its combined frequency. Now repeat the process combining the next two rightmost entries which may be symbols (leaves) or previously create nodes. This continues until you have just one node which is the head of your tree.
We are not going to bother to build the tree structure. We are only going to keep a list of the symbols that fall beneath a node. We are also going to realize that the combination of the two rightmost entries in the sorted list merely increases by one the bit length of each of the new node’s member symbols. When we finally reach the point where there is only one node in the list we would have assigned a bit length to every symbol based on its frequency. That is all we need to then create the codes for Huffman coding in DEFLATE format using the procedure for that outlined in the specification.
Here is where things really get confusing. This process doesn’t always create a DEFLATE compatible Huffman code set. Sometimes the bit length will exceed 15 (or 7 for the table later). We need a procedure for dealing with that. It amounts to being able to create a less than optimal Huffman tree with bit lengths limited to a maximum. This was a puzzle but I have a way to get it done.
So next I’ll take us through examples.
Let’s use an example. Here we have an alphabet of 19 symbols (0..18). The data set consists of 150 of these and after counting the occurrences of each we have the following. To make discussion simpler I will assign these symbols uppercase names. On the right are the results of the tally for each.
A 0x000 4 B 0x001 0 C 0x002 0 D 0x003 2 E 0x004 6 F 0x005 3 G 0x006 2 H 0x007 2 J 0x008 53 K 0x009 26 L 0x00a 5 M 0x00b 4 N 0x00c 3 P 0x00d 1 Q 0x00e 1 R 0x00f 1 S 0x010 37 T 0x011 0 U 0x012 0
In the standard approach to creating a Huffman table we ignore the symbols that do not appear in the data and arrange the other in order of decreasing frequency.
Used symbols: A D E F G H J K L M N P Q R S 4 2 6 3 2 2 53 26 5 4 3 1 1 1 37 Sorted by decreasing frequency: J S K E L A M F N D G H P Q R 53 37 26 6 5 4 4 3 3 2 2 2 1 1 1
Next we combine the lowest two frequency symbols into a new node with a combined total. I will name the nodes with lowercase characters just so you can track them. The shorter list is then resorted before proceeding to repeat. The process continues until this is only one node. Here I will show only the combining action for each step. We will get into more detail afterwards.
Starting set: J S K E L A M F N D G H P Q R 53 37 26 6 5 4 4 3 3 2 2 2 1 1 1 Step #1 combines Q and R into (a) with new frequency of 2. The list is resorted. J S K E L A M F N D G H (a) P 53 37 26 6 5 4 4 3 3 2 2 2 2 1 Step #2 combines (a) and P into (b) with new frequency of 3. J S K E L A M F N (b) D G H 53 37 26 6 5 4 4 3 3 3 2 2 2 Step #3 combines G and H into (c) with new frequency of 4. J S K E L A M (c) F N (b) D 53 37 26 6 5 4 4 4 3 3 3 2 Step #4 combines (b) and D into (d) with new frequency of 5. J S K E L (d) A M (c) F N 53 37 26 6 5 5 4 4 4 3 3 Step #5 combines F and N into (e) with new frequency of 6. J S K E (e) L (d) A M (c) 53 37 26 6 6 5 5 4 4 4 Step #6 combines M and (c) into (f) with new frequency of 8. J S K (f) E (e) L (d) A 53 37 26 8 6 6 5 5 4 Step #7 combines (d) and A into (g) with new frequency of 9. J S K (g) (f) E (e) L 53 37 26 9 8 6 6 5 Step #8 combines (e) and L into (h) with new frequency of 11. J S K (h) (g) (f) E 53 37 26 11 9 8 6 Step #9 combines (f) and E into (i) with new frequency of 14. J S K (i) (h) (g) 53 37 26 14 11 9 Step #10 combines (h) and (g) into (j) with new frequency of 20. J S K (j) (i) 53 37 26 20 14 Step #11 combines (j) and (i) into (k) with new frequency of 34. J S (k) K 53 37 34 26 Step #12 combines (k) and K into (m) with new frequency of 60. (m) J S 60 53 37 Step #13 combines J and S into (n) with new frequency of 90. (n) (m) 90 60 Step #14 combines (n) and (m) into our final node (p) with new frequency of 150. (p) 150 We are done.
Did you notice how nodes that we created were often quickly reused in another combination? This is what leads to a tree structure exceeding the maximum code length. Imagine a tree with one long branch down its right edge. It is very common when there are a few symbols that appear with high frequency and the balance are relatively low frequency symbols.
This combining nodes exercise was all well and good but something else needs to occur to make it useful. In the typical Huffman case in creating a node you would assign one combining nodes to the left link (bit = 0) and the other to the right link (bit = 1). This would then develop the tree structure that would work for you although most likely not to be DEFLATE compatible.
I am going to avoid the tree but note that in the act of combination all of the symbols participating will have their code length increased by 1. Combining leaves into a node creates another level in the tree. That’s what we are doing. In the code I will use a linked list to simply collect the symbols that are a member of (or lie below) any given node. In combining I will concatenate the member lists for the two leaves/nodes being combined and then increment the code length for each member.
For each step I going to show the node membership and the code length for our alphabet as we proceed through the process. Hopefully this table will make sense to you.
Step 1 2 3 4 5 6 7 8 9 10 11 12 13 14 clen A 0x000 4 0 0 0 0 0 0 0 1g 1g 1g 2j 3k 4m 4m 5p 5 D 0x003 2 0 0 0 0 1d 1d 1d 2g 2g 2g 3j 4k 5m 5m 6p 6 E 0x004 6 0 0 0 0 0 0 0 0 0 1i 1i 2k 3m 3m 4p 4 F 0x005 3 0 0 0 0 0 1e 1e 1e 2h 2h 3j 4k 5m 5m 6p 6 G 0x006 2 0 0 0 1c 1c 1c 2f 2f 2f 3i 3i 4k 5m 5m 6p 6 H 0x007 2 0 0 0 1c 1c 1c 2f 2f 2f 3i 3i 4k 5m 5m 6p 6 J 0x008 53 0 0 0 0 0 0 0 0 0 0 0 0 0 1n 2p 2 K 0x009 26 0 0 0 0 0 0 0 0 0 0 0 0 1m 1m 2p 2 L 0x00a 5 0 0 0 0 0 0 0 0 1h 1h 2j 3k 4m 4m 5p 5 M 0x00b 4 0 0 0 0 0 0 1f 1f 1f 2i 2i 3k 4m 4m 5p 5 N 0x00c 3 0 0 0 0 0 1e 1e 1e 2h 2h 3j 4k 5m 5m 6p 6 P 0x00d 1 0 0 1b 1b 2d 2d 2d 3g 3g 3g 4j 5k 6m 6m 7p 7 Q 0x00e 1 0 1a 2b 2b 3d 3d 3d 4g 4g 4g 5j 6k 7m 7m 8p 8 R 0x00f 1 0 1a 2b 2b 3d 3d 3d 4g 4g 4g 5j 6k 7m 7m 8p 8 S 0x010 37 0 0 0 0 0 0 0 0 0 0 0 0 0 1n 2p 2
In this table we follow the code length (clen) associated with each occurring symbol through the step by step combination process. Here as a symbol is combined into a new node (letter changes) we increment its bit depth or code length. The final column shows the resulting clen for this table.
So we mechanically have shown how to derive the code lengths for an alphabet symbol set with given frequencies. Next we create the DEFLATE Huffman code table for this.
My code to perform the node creation and code length incrementing looks something like this.
// Establish bit length for the Huffman table based upon frequencies
static int _bitlength(struct huff_t *tbl, int ncodes, int maxb)
{
uint16_t *list = MM_alloc(ncodes * sizeof(uint16_t), &_bitlength);
int *freq = MM_alloc(ncodes * sizeof(int), &_bitlength);
int nlist = 0;
int n, c, p;
int ret = TRUE;
// List all of the symbols used in the data along with their frequencies. Note that
// we store pointers +1 so as to keep 0 as a linked list terminator.
for (n = 0; n < ncodes; n++) if (tbl[n].cnt > 0)
{
list[nlist] = n + 1;
freq[nlist] = tbl[n].cnt;
nlist++;
}
// Note that there is a special boundary case when only 1 code is used. In this case
// the single code is encoded using 1 bit and not 0.
if (nlist == 1)
tbl[list[0] - 1].len = 1;
// process this list down to a single node
while (nlist > 1)
{
// sort the list by decreasing frequency
for (n = 0; n < nlist - 1; n++)
if (freq[n] < freq[n + 1]) { // swap order c = list[n]; list[n] = list[n + 1]; list[n + 1] = c; c = freq[n]; freq[n] = freq[n + 1]; freq[n + 1] = c; // need to sort back if (n > 0)
n -= 2;
}
// Combine the member lists associated with the last two entries. We combine the
// linked lists for the two low frequency nodes.
p = list[nlist - 2];
while (tbl[p - 1].link)
p = tbl[p - 1].link;
tbl[p - 1].link = list[nlist - 1];
// The new node has the combined frequency.
freq[nlist - 2] += freq[nlist - 1];
nlist--;
// Increase the code length for members of this node.
p = list[nlist - 1];
while (p)
{
tbl[p - 1].len++;
p = tbl[p - 1].link;
}
}
MM_free(freq);
MM_free(list);
return (ret);
}
You might note the check at line 20 handling a special case when there is only one used item in our alphabet. Here we need to use a code length of 1.
Now to be fair there is a lot more that I will be adding to this routine before we are done.
Now that we know the lengths of the code that we will be using to compress the data we can predict the compression ratio.
freq clen freq*clen
A 0x000 4 5 20
D 0x003 2 6 12
E 0x004 6 4 24
F 0x005 3 6 18
G 0x006 2 6 12
H 0x007 2 6 12
J 0x008 53 2 106
K 0x009 26 2 52
L 0x00a 5 5 25
M 0x00b 4 5 20
N 0x00c 3 6 18
P 0x00d 1 7 7
Q 0x00e 1 8 8
R 0x00f 1 8 8
S 0x010 37 2 74
-----------
416 bits (52 bytes)
If we multiply the frequency of a symbol times the code length and total that for the set we get total number of bits required to encode the original message. Originally we had 150 bytes or 1200 bits. When we are done we can store that same message in only 52 bytes. We’ve reduced the data to almost one third it’s original size.
Let’s see how to derive the bit codes that we will use in encoding the data.
We want to derive the actual binary code patterns for encoding this symbol set. The DEFLATE specification tells us to first count the number of codes for each code length.
N bl_count[N] 0 0 1 0 2 3 3 0 4 1 5 3 6 5 7 1 8 2
Next we find the numerical value of the smallest code for each code length. The following code is provided by the specification.
code = 0;
bl_count[0] = 0;
for (bits = 1; bits <= MAX_BITS; bits++) {
code = (code + bl_count[bits-1]) << 1;
next_code[bits] = code;
}
In performing this procedure we get the following. Here I will also show the codes in binary form.
N bl_count[N] next_code[N] 0 0 1 0 0 2 3 0 00 3 0 6 110 4 1 12 1100 5 3 26 11010 6 5 58 111010 7 1 126 1111110 8 2 254 11111110
Now we assign codes to each symbol based upon its length. The DEFLATE specification provides this code snippet. Basically the above defines the starting code which we increment after each use.
for (n = 0; n <= max_code; n++) {
len = tree[n].Len;
if (len != 0) {
tree[n].Code = next_code[len];
next_code[len]++;
}
}
And this ends up giving us the following codes for encoding this data.
freq clen code A 0x000 4 5 11010 D 0x003 2 6 111010 E 0x004 6 4 1100 F 0x005 3 6 111011 G 0x006 2 6 111100 H 0x007 2 6 111101 J 0x008 53 2 00 K 0x009 26 2 01 L 0x00a 5 5 11011 M 0x00b 4 5 11100 N 0x00c 3 6 111110 P 0x00d 1 7 1111110 Q 0x00e 1 8 11111110 R 0x00f 1 8 11111111 S 0x010 37 2 10
Take a few moments to picture what is going on. Basically with just 2 bits you can encode no more than 4 symbols. Since we have more than 4 symbols to encode we cannot use all 4 combinations of two bits. We reserve 1 or more bit combinations as a prefix indicting that an additional bit or more will be needed to identify other symbols. The decompressor will be processing the bit stream 1 bit at a time as it doesn’t know in advance how many bits will be needed to identify the next symbol.
In this symbol set it turns out that we use all but the last combination of two bits and 11b becomes the prefix accessing the rest of the symbol set. Note how this coincides with the 3 high frequency codes. It then turns out to be most efficient not to use any 3 bit codes and to jump right to 4 bits for the next possible symbol encoding. In fact if for any bit length if you reserve only the last combination as a prefix then the next bit length has only two combinations (a node). For 3 bit codes here that would be 110b and 111b. If we save all for prefix then we can encode more symbols. Here for the 4 bit codes there are 4 combinations: 1100b, 1101b, 1110b, and 1111b. Again this tree decided to use only one of the 4 bit combinations for a symbol.
Another thing to notice is that the final code for the largest bit length corresponds to the rightmost leaf in the tree. For DEFLATE that lexicographically is the longest code and requires a series of 1 bits to reach. So for this 8 bit code the last symbol is identified by 11111111b. This last code should always be 2**N – 1 where N is the largest bit length (code length). Note that ‘**’ indicates exponentiation here. Two is raised to the power of N.
If you think about it, the set of code lengths have to be just right to end up properly assigning codes to end up this way or to not overflow those available for any one bit length. This is assured by the procedure. If you try some random code lengths you will quickly see what I mean. In general you will be trying to create an impossible tree.
But wait!!
This table looks suspiciously like the code length encoding (third Huffman table that we have not discussed as yet). If it is, didn’t you mention that it would be limited to a bit depth or code length of 7? This one is 8 bits. Is that okay?
No. Is is not okay. You are right. I purposely chose this real-world example which actually does violate that code length rule. So this is not a DEFLATE compatible table. At least not for that third Huffman coding. This table occurs in trying to compress the /etc/JanosClasses.jarfile currently on my development JNIOR. And actually before this the literal table exceeds the 15 bit limit. The resulting compression fails.
Most of what you read now tells you to “adjust the Huffman tree” accordingly and prods on without a hint as to how you might do that. You can certainly detach and reattach nodes to get it done but how do you know that you haven’t significantly affected the compression ratio? You could punt and use the fixed Huffman tables afforded by another DEFLATE block type BTYPE 01. You know that you can’t just fiddle with the code lengths because you will end up trying to create an impossible tree. So what now?
Well, I can show you how to get it done.
Adjust the Huffman Tree Accordingly
We have created the optimum Huffman table for coding our data. Unfortunately we find out that it is not compatible for use with DEFLATE. The DEFLATE specification dictates that this particular table have a code length maximum of 7 bits. That being forced by the fact that these code lengths are stored in the DEFLATE stream using 3 bits each. That limits code lengths for this table to the set containing 0 thru 7.
Our table is too deep. It requires 8 bits to encode our data. What do we do about that? It seems that anything we do will reduce the efficiency of the compression. We need to create a less than optimum Huffman coding. How do we do that and keep the impact at a minimum? How do we not seriously damage the compression ratio?
We are going to adjust our Huffman table so that it does not exceed the maximum bit depth. Ideally we want to stop incrementing the code length of an symbols that reach the maximum. How can we properly do that? Well, we have to go back to the math. Let’s understand what makes a certain set of code lengths valid while others are not?
In the prior post we assigned code lengths to symbols in our alphabet based upon a tree construction algorithm. The steps in this algorithm are those that create a valid tree. It is not surprising then that our set of code lengths represent a real tree. As a result when we calculate the starting codes for each bit length the process ends up with usable codes. And as we noticed the last code in the tree is in fact 2**N – 1. In our case this is 2**8 -1 or 255 and in binary that being 11111111b.
Let me expand the loop in the starting code generation so we can see what happens. Here we will generate starting codes (S0..S8) for our code lengths. We will use a shorthand for the code length counts (N0..N8). In our example those are N = {0 0 3 0 1 3 5 1 2}. Note too that a left shift of 1 is equivalent to multiplication by 2. The starting codes (S) are calculated as follows:
S1 = (S0 + N0) << 1 = (0 + 0) << 1 = 2 * 0 = 0
S2 = (S1 + N1) << 1 = (0 + 0) << 1 = 2 * 0 = 0 00
S3 = (S2 + N2) << 1 = (0 + 3) << 1 = 2 * 3 = 6 110
S4 = (S3 + N3) << 1 = (6 + 0) << 1 = 2 * 6 = 12 1100
S5 = (S4 + N4) << 1 = (12 + 1) << 1 = 2 * 13 = 26 11010
S6 = (S5 + N5) << 1 = (26 + 3) << 1 = 2 * 29 = 58 111010
S7 = (S6 + N6) << 1 = (58 + 5) << 1 = 2 * 63 = 126 1111110
S8 = (S7 + N7) << 1 = (126 + 1) << 1 = 2 * 127 = 254 11111110
There are two things to notice here other than the fact that hist matches the table generated earlier. First, the count of 8 bit code lengths (N8) doesn’t come into play. Yet we know that there are 2 and the first will be assigned 11111110b and the second 11111111b. This being the 2**8 -1 that we now expect. The second thing is that all of the starting codes are even numbers. That being driven by the fact that they are the product of multiplication by 2. We will use this fact later.
Now I can reverse this procedure to generate starting codes back from the maximum bit length knowing that the last code must be 2**N – 1. So for this table we get the following:
S8 = 2**8 - N8 = 2**8 - 2 = 254
S7 = S8/2 - N7 = 254/2 - 1 = 127 - 1 = 126
S6 = S7/2 - N6 = 126/2 - 5 = 63 - 5 = 58
S5 = S6/2 - N5 = 58/2 - 3 = 29 - 3 = 26
S4 = S5/2 - N4 = 26/2 - 1 = 13 - 1 = 12
S3 = S4/2 - N3 = 12/2 - 0 = 6
S2 = S3/2 - N2 = 6/2 - 3 = 3 - 3 = 0
S1 = 0
S0 = 0
This is just a matter of running the calculations backwards and knowing (or realizing) that the last code has to be 2**N – 1. You can see it generates the same results.
Now what if we decide to not accept a bit depth exceeding the maximum? So we are going to force those two symbols wanting to be 8 bit codes to be two additional 7 bit codes. So our code length array will look like this: N = {0 0 3 0 1 3 5 3}. Here we combined S7 and S8 and eliminated 8 bit altogether. Legal? Of course not. You can’t visualize what that does to a tree. let’s try the calculations back from the new maximum of 2**7 – 1.
S7 = 2**7 - N7 = 128 - 3 = 125
Here this fails immediately. We know that starting codes (S) must be even numbers and 125 is odd! Not surprising as we are kind of floating a pair of leaves up in the air somehow. Can we make a home for them?
Clearly if we were to reattach those leaves somewhere else in the tree structure other nodes must be increased in bit depth. We need another 7 bit symbol to get S7 to be an even 124. To do that with minimum impact on compression ratio we increase the 6 bit coded symbol with the lowest frequency to 7 bits. Our array now being N = {0 0 3 0 1 3 4 4}. Try again:
S7 = 2**7 - N7 = 128 - 4 = 124
S6 = 124/2 - N6 = 62 - 4 = 58
S5 = S6/2 - N5 = 58/2 - 3 = 29 - 3 = 26
S4 = S5/2 - N4 = 26/2 - 1 = 13 - 1 = 12
S3 = S4/2 - N3 = 12/2 - 0 = 6
S2 = S3/2 - N2 = 6/2 - 3 = 3 - 3 = 0
S1 = 0
S0 = 0
Um. Everything seemed to fit right in. Is this tree valid? Let’s see.
N bl_count[N] next_code[N] 0 0 1 0 0 2 3 0 00 3 0 6 110 4 1 12 1100 5 3 26 11010 6 4 58 111010 7 4 124 1111100
freq clen code A 0x000 4 5 11010 D 0x003 2 6 111010 E 0x004 6 4 1100 F 0x005 3 6 111011 G 0x006 2 6 111100 H 0x007 2 6 111101 J 0x008 53 2 00 K 0x009 26 2 01 L 0x00a 5 5 11011 M 0x00b 4 5 11100 N 0x00c 3 7 1111100 P 0x00d 1 7 1111101 Q 0x00e 1 7 1111110 R 0x00f 1 7 1111111 S 0x010 37 2 10
This appears to have successfully generated a Huffman tree that would work with DEFLATE format! Let’s look at the compression ratio for this.
freq clen freq*clen
A 0x000 4 5 20
D 0x003 2 6 12
E 0x004 6 4 24
F 0x005 3 6 18
G 0x006 2 6 12
H 0x007 2 6 12
J 0x008 53 2 106
K 0x009 26 2 52
L 0x00a 5 5 25
M 0x00b 4 5 20
N 0x00c 3 7 21
P 0x00d 1 7 7
Q 0x00e 1 7 7
R 0x00f 1 7 7
S 0x010 37 2 74
-----------
417 bits (53 bytes)
Wait! This only cost us 1 bit? Yes it did but to store it we would need another whole byte. So the impact of this procedure is likely (though not proven) to have a minimum impact on compression ratio. Yet, it corrects the table to insure that it is compatible with DEFLATE.
To generalize the process, the reversed starting code calculation is repeated from 2**N – 1 when N is the maximum bit depth back to 0 for bit length 0. If at any point the calculated starting code is not even, you must set the bit depth for the next least frequent symbol to include it at this code length and make the starting code even.
In my next post I will show code for this.
The complete procedure for generating a DEFLATE format compatible Huffman table limited to a maximum bit depth is shown here. I know that this is not optimized code. There is some unnecessary execution but I had wanted to keep steps separate and clear. You can be sure that over time I will optimize the coding and obfuscate it suitably for all future generations.
This routine has the capacity to return FALSE if a table cannot be created. It was doing just that when the bit depth (code length) exceeded maximum. That has since been corrected. It will always return TRUE now.
// Establish bit length for the Huffman table based upon frequencies
static int _bitlength(struct huff_t *tbl, int ncodes, int maxb)
{
uint16_t *list = MM_alloc(ncodes * sizeof(uint16_t), &_bitlength);
int *freq = MM_alloc(ncodes * sizeof(int), &_bitlength);
int nlist = 0;
int n, c, p;
int ret = TRUE;
uint16_t *ptr;
// List all of the symbols used in the data along with their frequencies. Note that
// we store pointers +1 so as to keep 0 as a linked list terminator.
for (n = 0; n < ncodes; n++) if (tbl[n].cnt > 0)
{
list[nlist] = n + 1;
freq[nlist] = tbl[n].cnt;
nlist++;
}
// Note that there is a special boundary case when only 1 code is used. In this case
// the single code is encoded using 1 bit and not 0.
if (nlist == 1)
tbl[list[0] - 1].len = 1;
// process this list down to a single node
while (nlist > 1)
{
// sort the list by decreasing frequency
for (n = 0; n < nlist - 1; n++)
if (freq[n] < freq[n + 1]) { // swap order c = list[n]; list[n] = list[n + 1]; list[n + 1] = c; c = freq[n]; freq[n] = freq[n + 1]; freq[n + 1] = c; // need to sort back if (n > 0)
n -= 2;
}
// Combine the member lists associated with the last two entries. We combine the
// linked lists for the two low frequency nodes.
p = list[nlist - 2];
while (tbl[p - 1].link)
p = tbl[p - 1].link;
tbl[p - 1].link = list[nlist - 1];
// The new node has the combined frequency.
freq[nlist - 2] += freq[nlist - 1];
nlist--;
// Sort the members of this node by decreasing code length. Longer codes to the
// left. This will also sort the frequency of the symbols in increasing order
// when code lengths are equal. We need this arrangement for the next step should
// we be required to balance the tree and avoid exceeding the maximum code
// length (maxb).
p = TRUE;
while (p)
{
p = FALSE;
ptr = &list[nlist - 1];
while (*ptr && tbl[*ptr - 1].link)
{
c = tbl[*ptr - 1].link;
if ((tbl[*ptr - 1].len < tbl[c - 1].len) || (tbl[*ptr - 1].len == tbl[c - 1].len && tbl[*ptr - 1].cnt > tbl[c - 1].cnt))
{
n = tbl[c - 1].link;
tbl[*ptr - 1].link = n;
tbl[c - 1].link = *ptr;
*ptr = c;
p = TRUE;
}
ptr = &tbl[*ptr - 1].link;
}
}
// Increase the code length for members of this node. We cannot exceed the maximum
// code length (maxb).
p = list[nlist - 1];
while (p)
{
if (tbl[p - 1].len < maxb)
tbl[p - 1].len++;
p = tbl[p - 1].link;
}
// Now verify the structure. This should be absolutely proper up until the point when
// we prevent code lengths from exceeding the maximum. Once we do that we are likely
// creating an impossible tree. We will need to correct that.
p = list[nlist - 1];
c = tbl[p - 1].len;
if (c == maxb)
{
n = 1 << c;
while (p)
{
if (tbl[p - 1].len == c)
n--;
else
{
// n must be even at this point or we extend the length group
if (n & 1)
{
tbl[p - 1].len = c;
n--;
}
else
{
c--;
n /= 2;
}
}
p = tbl[p - 1].link;
}
}
}
MM_free(freq);
MM_free(list);
return (ret);
}
Here are the steps that it performs:
- Create an array for all used alphabet symbols (those with non-zero frequency).
- Check for the special case where there is only one symbol. In that case we use a 1 bit code where one is unused.
- Sort the list array by decreasing frequency. The least frequent symbols are then at the end of the list.
- Combine the rightmost two least frequent symbols or nodes into a single new node having the combined frequency. All members of the two combined nodes become members of the new node.
- Sort the member list for the new node by decreasing bit depth (current code length) and secondly by increasing frequency.
- Increase the bit depth for all members of the new node by 1. If a symbol will exceed the maximum bit depth do not increment it.
- If we have reached the maximum bit depth then confirm the tree structure using the reverse starting code length calculations. Elevate the next least frequent symbol to the current bit depth if the calculated starting code is not an even number. Check all code lengths.
- If there is more than one entry in the list array (not down to one node yet) then repeat at Step #3.
So to review….
First, we covered how to perform a reasonably fast version of LZ77. This filling a 64 KB buffer with compressed data which contains literals and length-distance codes.
When we need to we will flush the 64 KB buffer and generate a block of DEFLATE format. At that point we call a routine that first analyzes the data for code frequencies. There are to be two alphabets. One for literals and length codes. The other for distance codes.
Now we’ve developed a method for generating DEFLATE compatible Huffman tables for our two alphabets. The bulk of the complexity is now behind us but there is still some work to do before we can start generate our compressed bit stream.
Moving on…
Now we need the size of our literal alphabet (HLIT) and our distance alphabet (HDIST) since it is unlikely the we have utilized all literal symbols (0..285) or distance codes (0..29). So here we scan each to trim unused symbols.
// Now we combine the bit length arrays into a single array for run-length-like repeat encoding.
// In DEFLATE this encoding can overlap for the literal table to the distance code table as
// if a single array. First determine the alphabet size for each table.
for (hlit = 286; 0 < hlit; hlit--)
if (littbl[hlit - 1].len > 0)
break;
for (hdist = 30; 0 < hdist; hdist--)
if (dsttbl[hdist - 1].len > 0)
break;
So we have the two alphabets. One for literals and length codes (0..HLIT) and one for distance codes (0..HDIST). We’ve seen that all we need are the code lengths for each symbol set to define the associated Huffman tree. We need to convey this information to the decompressor. The DEFLATE format combines the code length arrays for the two alphabets now into one long array of HLIT + HDIST code lengths.
// Now create the bit length array
cntlist = MM_alloc((hlit + hdist) * sizeof(int), &_bufflush);
for (n = 0; n < hlit; n++)
cntlist[n] = littbl[n].len;
for (n = 0; n < hdist; n++)
cntlist[hlit + n] = dsttbl[n].len;
Now we know that the end-of-block code (256) is used as well as at least a handful of length codes and distance codes. So this array of code lengths itself is fairly long. It will be somewhere between 260 and 315 entries. Each code length is is in the set 0..15. So typically there is a lot of repetition. There can be a large number of 0’s in a row. Consider data that is constrained to 7-bit ASCII. In that case there are 128 literal codes that never occur and would have a code length of 0.
The DEFLATE specification defines a kind of run-length encoding for this array. This encodes sequences of code lengths using three additional codes.
The Huffman codes for the two alphabets appear in the block
immediately after the header bits and before the actual
compressed data, first the literal/length code and then the
distance code. Each code is defined by a sequence of code
lengths, as discussed in Paragraph 3.2.2, above. For even
greater compactness, the code length sequences themselves are
compressed using a Huffman code. The alphabet for code lengths
is as follows:
0 - 15: Represent code lengths of 0 - 15
16: Copy the previous code length 3 - 6 times.
The next 2 bits indicate repeat length
(0 = 3, ... , 3 = 6)
Example: Codes 8, 16 (+2 bits 11),
16 (+2 bits 10) will expand to
12 code lengths of 8 (1 + 6 + 5)
17: Repeat a code length of 0 for 3 - 10 times.
(3 bits of length)
18: Repeat a code length of 0 for 11 - 138 times
(7 bits of length)
So as you can see we are heading towards our third Huffman table. This one with an alphabet of 19 codes (0..18). That’s why the symbol set I used for the example in handling maximum code length has 19 members. I used one of these tables as an example.
In my next post I will show the procedure I use for applying the repeat codes in this alphabet.
The current version of jniorsys.log on my development JNIOR compresses into a single block using the following literal and distance tables.
littbl
0x00a 2 11 11111101110
0x00d 2 12 111111111000
0x020 93 6 101000
0x027 4 11 11111101111
0x028 14 9 111101010
0x029 3 11 11111110000
0x02a 2 12 111111111001
0x02b 9 10 1111101000
0x02c 9 10 1111101001
0x02d 23 8 11101100
0x02e 158 5 01100
0x02f 18 9 111101011
0x030 120 6 101001
0x031 182 5 01101
0x032 147 5 01110
0x033 150 5 01111
0x034 127 6 101010
0x035 132 6 101011
0x036 113 6 101100
0x037 110 6 101101
0x038 113 6 101110
0x039 106 6 101111
0x03a 91 6 110000
0x03c 2 12 111111111010
0x03d 3 11 11111110001
0x03e 3 11 11111110010
0x041 6 10 1111101010
0x043 5 11 11111110011
0x044 1 13 1111111111100
0x046 2 12 111111111011
0x048 1 13 1111111111101
0x04a 3 11 11111110100
0x04c 3 11 11111110101
0x04d 5 11 11111110110
0x04e 4 11 11111110111
0x04f 5 10 1111101011
0x050 11 9 111101100
0x052 10 9 111101101
0x053 6 10 1111101100
0x054 5 10 1111101101
0x055 2 12 111111111100
0x057 3 11 11111111000
0x05a 1 13 1111111111110
0x05f 5 10 1111101110
0x061 44 7 1101100
0x062 7 10 1111101111
0x063 19 9 111101110
0x064 30 8 11101101
0x065 52 7 1101101
0x066 14 9 111101111
0x067 13 9 111110000
0x068 9 10 1111110000
0x069 45 7 1101110
0x06a 6 10 1111110001
0x06b 3 11 11111111001
0x06c 29 8 11101110
0x06d 21 8 11101111
0x06e 46 7 1101111
0x06f 51 7 1110000
0x070 31 8 11110000
0x071 2 12 111111111101
0x072 37 8 11110001
0x073 27 8 11110010
0x074 40 7 1110001
0x075 16 9 111110001
0x076 6 10 1111110010
0x077 8 10 1111110011
0x078 4 11 11111111010
0x079 9 10 1111110100
0x07a 4 11 11111111011
0x100 1 13 1111111111111
0x101 1248 2 00
0x102 580 4 0100
0x103 168 5 10000
0x104 160 5 10001
0x105 72 7 1110010
0x106 119 6 110001
0x107 82 6 110010
0x108 17 9 111110010
0x109 116 6 110011
0x10a 253 5 10010
0x10b 120 6 110100
0x10c 52 7 1110011
0x10d 69 7 1110100
0x10e 79 6 110101
0x10f 20 8 11110011
0x110 54 7 1110101
0x111 236 5 10011
0x112 371 4 0101
0x113 34 8 11110100
0x114 6 10 1111110101
0x115 17 9 111110011
0x116 6 10 1111110110
dsttbl
0x002 1 10 1111111100
0x003 2 10 1111111101
0x008 2 10 1111111110
0x009 2 10 1111111111
0x00a 14 8 11111110
0x00b 204 4 0100
0x00c 225 4 0101
0x00d 46 7 1111110
0x00e 168 5 11100
0x00f 85 6 111110
0x010 202 4 0110
0x011 130 5 11101
0x012 193 4 0111
0x013 146 5 11110
0x014 259 4 1000
0x015 209 4 1001
0x016 301 4 1010
0x017 255 4 1011
0x018 377 3 000
0x019 293 4 1100
0x01a 433 3 001
0x01b 332 4 1101
We determine HLIT and HDIST for this and combine the code lengths into one HLIT + HDIST length array.
HLIT: 279 HDIST: 28 0 0 0 0 0 0 0 0 0 0 11 0 0 12 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 11 9 11 12 10 10 8 5 9 6 5 5 5 6 6 6 6 6 6 6 0 12 11 11 0 0 10 0 11 13 0 12 0 13 0 11 0 11 11 11 10 9 0 9 10 10 12 0 11 0 0 13 0 0 0 0 10 0 7 10 9 8 7 9 9 10 7 10 11 8 8 7 7 8 12 8 8 7 9 10 10 11 10 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 13 2 4 5 5 7 6 6 9 6 5 6 7 7 6 8 7 5 4 8 10 9 10 0 0 10 10 0 0 0 0 10 10 8 4 4 7 5 6 4 5 4 5 4 4 4 4 3 4 3 4
So this array has 307 entries and you can see that there is a lot of repetition. We next apply the repeat codes as appropriate to shorten this array to 139 entries.
HLIT: 279 HDIST: 28 0 0 0 0 0 0 0 0 0 0 11 0 0 12 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 11 9 11 12 10 10 8 5 9 6 5 5 5 6 6 6 6 6 6 6 0 12 11 11 0 0 10 0 11 13 0 12 0 13 0 11 0 11 11 11 10 9 0 9 10 10 12 0 11 0 0 13 0 0 0 0 10 0 7 10 9 8 7 9 9 10 7 10 11 8 8 7 7 8 12 8 8 7 9 10 10 11 10 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 13 2 4 5 5 7 6 6 9 6 5 6 7 7 6 8 7 5 4 8 10 9 10 0 0 10 10 0 0 0 0 10 10 8 4 4 7 5 6 4 5 4 5 4 4 4 4 3 4 3 4 NCNT: 139 17/7 11 0 0 12 18/7 6 17/3 11 9 11 12 10 10 8 5 9 6 5 5 5 6 16/3 0 12 11 11 0 0 10 0 11 13 0 12 0 13 0 11 0 11 11 11 10 9 0 9 10 10 12 0 11 0 0 13 17/1 10 0 7 10 9 8 7 9 9 10 7 10 11 8 8 7 7 8 12 8 8 7 9 10 10 11 10 11 18/122 13 2 4 5 5 7 6 6 9 6 5 6 7 7 6 8 7 5 4 8 10 9 10 0 0 10 10 17/1 10 10 8 4 4 7 5 6 4 5 4 5 4 16/0 3 4 3 4
Here when one of the repeat codes are used I show the value of the extra bits we will insert following the Huffman code for the symbol.
Now we create the Huffman table for this array and determine frequencies. Note that extra bits are inserted later and are not part of the Huffman encoding. Here the maximum code length is 7 bits.
// Ugh. Now we need yet another Huffman table for this run-length alphabet. First we establish
// the frequencies. Note that we skip the byte defining the extra bits.
cnttbl = MM_alloc(HUFF_HLEN * sizeof(struct huff_t), &_bufflush);
for (n = 0; n < ncnt; n++)
{
cnttbl[cntlist[n]].cnt++;
if (cntlist[n] >= 16)
n++;
}
// We need to determine the bit lengths.
if (!_bitlength(cnttbl, HUFF_HLEN, 7))
{
err = TRUE;
break;
}
This results in the following third Huffman table that we will use to code the code lengths which in turn are used to generate the literal and distance tables for the data compression.
cnttbl 0x000 17 3 000 0x002 1 6 111100 0x003 2 6 111101 0x004 9 4 1000 0x005 11 3 001 0x006 9 4 1001 0x007 11 4 1010 0x008 10 4 1011 0x009 10 4 1100 0x00a 19 3 010 0x00b 14 3 011 0x00c 6 4 1101 0x00d 4 5 11100 0x010 2 6 111110 0x011 4 5 11101 0x012 2 6 111111
Are we there yet?
Well, we are getting close.
As before we will need to convey the code lengths in this ‘cnttbl’ to the decompressor. We have N = {3 0 6 6 4 3 4 4 4 4 3 3 4 5 0 0 6 5 6}. I mentioned earlier that these are stored each with 3 bits in the bit stream limiting the code length to 7 bits.
But DEFLATE wants to save every possible byte. Each of these code lengths has a probability of being used over some general set of data types. They decided to sequence these into an array i a custom order such that the least likely to be used code lengths fall at the end and can be trimmed. So we get the order from the specification and sequence these. Notice that our three 0 bit code length do in fact get trimmed.
// Finally (haha) we establish a custom order for these bit lengths
// array defined above
//static const char hclen_order[HUFF_HLEN] = {
// 16, 17, 18, 0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2,
// 14, 1, 15
//};
bitlens = MM_alloc(HUFF_HLEN * sizeof(int), &_bufflush);
for (n = 0; n < HUFF_HLEN; n++)
bitlens[n] = cnttbl[hclen_order[n]].len;
// Now the the end of this array should be 0's so we find a length for the array
for (hclen = HUFF_HLEN; 0 < hclen; hclen--)
if (bitlens[hclen - 1] > 0)
break;
6 5 6 3 4 4 4 4 3 3 3 4 4 6 5 6 0 0 0 HCLEN: 16
It is hard to believe but we now have everything that we need to actually generate the compressed bit stream. Well, all except a couple of routines to actually do the serialization. So that will be the next step.
We’re going to output to a bit stream. Each write will likely involve a different number of bits. Someplace we have to properly sequence these into bytes to append to the output buffer.
To do this we need one routine to write called _writeb() and one to use at the end to flush any remaining unwritten bits called _flushb().
// Routine to stream bits
static void _writeb(int num, int code, struct bitstream_t *stream)
{
// if no bits then nothing to do
if (num == 0)
return;
// insert bits into the stream
code &= ((1 << num) - 1);
code <<= stream->nbits;
stream->reg |= code;
stream->nbits += num;
// stream completed bytes
while (stream->nbits >= 8)
{
stream->buffer[stream->length++] = (stream->reg & 0xff);
stream->reg >>= 8;
stream->nbits -= 8;
}
}
// Routine flushes the bitstream
static void _flushb(struct bitstream_t *stream)
{
if (stream->nbits)
{
stream->buffer[stream->length++] = (stream->reg & 0xff);
stream->reg = 0;
stream->nbits = 0;
}
}
So to tie this together we use a structure.
// structure to assist with bit streaming
struct bitstream_t {
char *buffer;
int length;
uint32_t reg;
int nbits;
};
This seems simple enough but there are a couple things to understand. The DEFLATE specification gets into it right off the bat.
The first bit of the bit stream is the least significant bit of the first byte in the buffer. Once 8 bits are retrieved the 9th is the least significant bit of the second byte and so on.
A value appears in the stream starting with it’s least significant bit. That means that the bit order does not need to be reversed to pack the value at the tail of the current bit stream.
Huffman codes are processed a bit at a time. When you are reading a Huffman code you do not know how many bits you will need to retrieve the code for a valid symbol in the alphabet. So in this case you must insert the Huffman code so the most-significant bit is read first. The order of Huffman bits needs to be reversed. Armed with that fact, I have stored these codes in the tables in reverse order. That will be apparent in the following code to generate the tables for coding.
So the last thing we need to do is generate the actual Huffman codes for the three tables.
// Now we need Huffman codes for these tables because eventually someday we will actually be
// generating a compressed bit stream.
// Next we total the number of symbols using each bit length. These will be used to assign
// bit codes for each alphabet symbol.
litcnts = MM_alloc(16 * sizeof(int), &_bufflush);
for (n = 0; n < 286; n++)
if (littbl[n].len > 0)
litcnts[littbl[n].len]++;
dstcnts = MM_alloc(16 * sizeof(int), &_bufflush);
for (n = 0; n < 30; n++)
if (dsttbl[n].len > 0)
dstcnts[dsttbl[n].len]++;
bitcnts = MM_alloc(16 * sizeof(int), &_bufflush);
for (n = 0; n < HUFF_HLEN; n++)
if (cnttbl[n].len)
bitcnts[cnttbl[n].len]++;
// Now we calculate starting codes for each bit length group. This procedure is defined in the
// DEFLATE specification. We can define the Huffman tables in a compressed format provided that
// the Huffman tables follow a couple of additional rules. Using these starting codes we
// can assing codes for each alphabet symbol. Note that Huffman codes are processed bit-by-bit
// and therefore must be generated here in reverse bit order.
// Define codes for the literal Huffman table
startcd = MM_alloc(16 * sizeof(int), &_bufflush);
for (n = 0; n < 15; n++)
startcd[n + 1] = (startcd[n] + litcnts[n]) << 1;
for (n = 0; n < 286; n++)
{
len = littbl[n].len;
if (len)
{
c = startcd[len]++;
while (len--)
{
littbl[n].code <<= 1;
littbl[n].code |= (c & 1);
c >>= 1;
}
}
}
// Define codes for the distance Huffman table
for (n = 0; n < 15; n++)
startcd[n + 1] = (startcd[n] + dstcnts[n]) << 1;
for (n = 0; n < 30; n++)
{
len = dsttbl[n].len;
if (len)
{
c = startcd[len]++;
while (len--)
{
dsttbl[n].code <<= 1;
dsttbl[n].code |= (c & 1);
c >>= 1;
}
}
}
// Define codes for the bit length Huffman table
for (n = 0; n < 15; n++)
startcd[n + 1] = (startcd[n] + bitcnts[n]) << 1;
for (n = 0; n < HUFF_HLEN; n++)
{
len = cnttbl[n].len;
if (len)
{
c = startcd[len]++;
while (len--)
{
cnttbl[n].code <<= 1;
cnttbl[n].code |= (c & 1);
c >>= 1;
}
}
}
Coming up next: Actually Generating the Bit Stream
The DEFLATE specification greatly oversimplifies the whole process by defining the block format in about a single page.
We can now define the format of the block:
5 Bits: HLIT, # of Literal/Length codes - 257 (257 - 286)
5 Bits: HDIST, # of Distance codes - 1 (1 - 32)
4 Bits: HCLEN, # of Code Length codes - 4 (4 - 19)
(HCLEN + 4) x 3 bits: code lengths for the code length
alphabet given just above, in the order: 16, 17, 18,
0, 8, 7, 9, 6, 10, 5, 11, 4, 12, 3, 13, 2, 14, 1, 15
These code lengths are interpreted as 3-bit integers
(0-7); as above, a code length of 0 means the
corresponding symbol (literal/length or distance code
length) is not used.
HLIT + 257 code lengths for the literal/length alphabet,
encoded using the code length Huffman code
HDIST + 1 code lengths for the distance alphabet,
encoded using the code length Huffman code
The actual compressed data of the block,
encoded using the literal/length and distance Huffman
codes
The literal/length symbol 256 (end of data),
encoded using the literal/length Huffman code
The code length repeat codes can cross from HLIT + 257 to the
HDIST + 1 code lengths. In other words, all code lengths form
a single sequence of HLIT + HDIST + 258 values.
There are a couple of reasons why the suggestion to teach JANOS how to compress files has been in Redmine for 5 years. That’s about how long ago when in development JANOS began to directly use JAR files for application programming. The obvious reason that it took 5 years to implement is that there really isn’t a huge need for compression in JNIOR. Storage was limited in the previous series and if you had wanted to keep log files around for any serious length of time it would have helped if we could compress them. The Series 4 has much more storage but still not a lot by today’s standards.
The real reason you may now realize. It is a bit involved. Given that JANOS uses no third party developed code and that I had not been able to find usable reference materials (search engines having been damaged by marketing greed).There were some hurdles that left this suggestion sit on the list at a low priority for practically ever. Well, we’ve got it done now.
Let’s generate the bit stream and be done with this tome.
First we stream the Block Header. The very first bit indicates whether or not the block is the last for the compression. For the last block this BFINAL bit will be a 1. It is 0 otherwise. We also are using the dynamic Huffman table type. The next two bits indicate the block type BTYPE. Here we use 10b as we will be providing our own Huffman tables. Yeah, we could have taken the easy path and used a fixed set of tables (BTYPE 01b) but that is no fun.
// Now we have codes and everything that we need (Finally!) to generate the compressed bit
// stream.
// set BFINAL and type BTYPE of 10
_writeb(1, final ? 1 : 0, stream);
_writeb(2, 0x02, stream);
We have already determined the sizes of our alphabets. We have HLIT defining the size of the literal alphabet that includes codes for sequence lengths. The complete alphabet space covers the range 0..285 but since we are not likely to use them all HLIT defines how many actually are used (0..HLIT). We also have HDIST playing a similar role for the distance alphabet which could range 0..29.
Those two parameters are supplied next. Here each values is conveyed in 5 bits. We can do that since we know that HDIST has to be at least 257 since we do have to use the end-of-block code of 256 in our alphabet. So we supply really the count to length codes used which is similar in magnitude to teh count of distance codes. So HLIT is supplied as HLIT – 257 and HDIST as HDIST – 1.
// Now we output HLIT, HDIST, and HCLEN
_writeb(5, hlit - 257, stream);
_writeb(5, hdist - 1, stream);
_writeb(4, hclen - 4, stream);
// Output the HCLEN counts from the bit length array. Note that we have already ordered it
// as required.
for (n = 0; n < hclen; n++)
_writeb(3, bitlens[n], stream);
Following the delivery of HLIT and HDIST we supply HCLEN as HCLEN – 4. Recall that HCLEN defines the size of alphabet we are going to use to encode the array of code lengths for the main two Huffman tables. HCLEN defines the the number of elements we are going to supply for that 19 element array that has the custom order. The balance beyond HCLEN elements is assumed to be 0. This is the array whose elements are supplied with 3 bits and thus limited to the range 0..7. We include HCLEN elements simply as shown above.
Next we stream the concatenated array of code lengths. This array has HLIT + HDIST elements that have been compressed using repeat codes. Here we output the compressed array using the 19 symbol alphabet that we just defined for the decompressor by sending the array above. We encounter the extra bits usage for the first time. You can see in the following that after streaming the repeat codes 16, 17 or 18 we insert the field specifying the repeat count using the required number of extra bits.
// Output the run-length compressed HLIT + HDIST code lengths using the code length
// Huffman codes. The two tables are blended together in the run-length encoding.
// Note that we need to insert extra bits where appropriate.
for (n = 0; n < ncnt; n++)
{
c = cntlist[n];
_writeb(cnttbl[c].len, cnttbl[c].code, stream);
if (c >= 16)
{
switch (c)
{
case 16:
_writeb(2, cntlist[++n], stream);
break;
case 17:
_writeb(3, cntlist[++n], stream);
break;
case 18:
_writeb(7, cntlist[++n], stream);
break;
}
}
}
If you are the decompressor at this point you have everything you need to develop the Huffman tables for literals and distance codes. You had to expand thee repeat compression and separate the two code length sets. You then tallied code length counts and calculated starting codes for each bit length. Finally you assigned codes to each used alphabet symbol. So we are ready to deal with the actual compressed data.
When we initially scanned the LZ77 compressed data to determine frequencies we had to temporarily expand the length-distance references to determine which codes from the length and distance alphabets we would be using. Well the following loop is practically identical because we again process the LZ77 compressed data expanding the length-distance references. This time we will output the codes to the bit stream. Here again we have the extra bits to insert. Where we ignored them before, now we insert them into the stream when necessary.
// Unbelievable! We can actually now output the compressed data for the block! This is
// encoded using the literal and distance Huffman tables as required. Note we need to
// again process the escaping and length-distance codes.
for (n = 0; n < osize; n++)
{
c = obuf[n];
if (c != 0xff)
_writeb(littbl[c].len, littbl[c].code, stream);
else
{
// check and tally escaped 0xff
if (obuf[++n] == 0xff)
_writeb(littbl[0xff].len, littbl[0xff].code, stream);
else
{
// table defined above
//static const int lcode_ofs[29] = {
// 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 15, 17, 19, 23, 27, 31,
// 35, 43, 51, 59, 67, 83, 99, 115, 131, 163, 195, 227, 258
//};
// determine required length code for lengths (3..258). This code is
// coded in the literal table.
len = (obuf[n++] & 0xff) + 3;
for (c = 0; c < 29; c++)
if (lcode_ofs[c] > len)
break;
code = 256 + c;
_writeb(littbl[code].len, littbl[code].code, stream);
// insert extra bits as required by the code
// table defined above
//static const int lcode_bits[29] = {
// 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
// 3, 4, 4, 4, 4, 5, 5, 5, 5, 0
//};
c = lcode_bits[code - 257];
if (c)
_writeb(c, len - lcode_ofs[code - 257], stream);
// table define above
//static const int dcode_ofs[30] = {
// 1, 2, 3, 4, 5, 7, 9, 13, 17, 25, 33, 49, 65, 97, 129, 193,
// 257, 385, 513, 769, 1025, 1537, 2049, 3073, 4097, 6145,
// 8193, 12289, 16385, 24577
//};
// determine required distance code for distances (1..32768). This code is
// coded in the distance table.
dst = (obuf[n++] & 0xff) << 8;
dst |= (obuf[n] & 0xff);
for (c = 0; c < 30; c++)
if (dcode_ofs[c] > dst)
break;
code = c - 1;
_writeb(dsttbl[code].len, dsttbl[code].code, stream);
// insert extra bits as required by the code
// table defined above
//static const int dcode_bits[30] = {
// 0, 0, 0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8,
// 9, 9, 10, 10, 11, 11, 12, 12, 13, 13
//};
c = dcode_bits[code];
if (c)
_writeb(c, dst - dcode_ofs[code], stream);
}
}
}
And finally we output that end-of-block code (256). If BFINAL were set and this were the last block in the compression (LZ77 flushing the last partial buffer of data) we would flush the serial buffer. This provides a final byte with the remaining bits for the stream.
// And finally the end-of-block code and flush
_writeb(littbl[256].len, littbl[256].code, stream);
if (final)
_flushb(stream);
At this point the buffer supplied by the LZ77 compression has been flushed to the bit stream. We would reset that buffer pointer and return. If there is more data the LZ77 compressor will then proceed with it. Remember that I had defined this buffer to be 64KB so there will likely be more in the case of larger files.
This DEFLATE compression capability will be part of JANOS v1.6.4 and later OS. I am likely to do some optimization before release. Here we see that it works. I’ll create an archive containing the files in my JNIOR’s root folder.
bruce_dev /> zip -c test.zip /
6 files saved
bruce_dev />
bruce_dev /> zip test.zip
Size Packed CRC32 Modified
56096 10764 81% 0b779605 Jan 31 2018 08:42 jniorsys.log
40302 6249 84% b1dffc05 Jan 26 2018 07:38 web.log
22434 9499 58% 059a09d9 Jan 25 2018 14:53 manifest.json
89 89 0% f97bbba2 Jan 28 2018 09:11 access.log
990 460 54% 9699bbfe Jan 30 2018 14:48 jniorboot.log.bak
990 461 53% 8f3c0390 Jan 31 2018 08:42 jniorboot.log
6 files listed
bruce_dev />
This archive verifies. This verification does decompress each file and confirm the CRC32.
bruce_dev /> zip -vl test.zip verifying: jniorsys.log (compressed) verifying: web.log (compressed) verifying: manifest.json (compressed) verifying: access.log verifying: jniorboot.log.bak (compressed) verifying: jniorboot.log (compressed) 6 entries found - content verifies! bruce_dev />
We can repeat the construction in verbose output mode. Here we see timing. Again, keep in mind that JANOS is running on a 100 MHz Renesas RX63N micro-controller.
bruce_dev /> zip -cl test.zip / deflate: /jniorsys.log (56096 bytes) saving: jniorsys.log (compressed 80.8%) 1.176 secs deflate: /web.log (40302 bytes) saving: web.log (compressed 84.5%) 0.671 secs deflate: /manifest.json (22434 bytes) saving: manifest.json (compressed 57.7%) 1.863 secs saving: access.log (stored) 0.011 secs deflate: /jniorboot.log.bak (990 bytes) saving: jniorboot.log.bak (compressed 53.5%) 0.054 secs deflate: /jniorboot.log (990 bytes) saving: jniorboot.log (compressed 53.4%) 0.054 secs 6 files saved bruce_dev />
The /etc/JanosClasses.jar file compresses and this file is where I first encountered Huffman tables whose bit depth (code length) exceeded the DEFLATE maximums (15 bit for literal and distance tables, 7 bit for code length encoding).
bruce_dev /> zip -cl test.zip /etc
deflate: /etc/JanosClasses.jar (266601 bytes)
saving: etc/JanosClasses.jar (compressed 11.2%) 24.215 secs
1 files saved
bruce_dev />
bruce_dev /> zip test.zip
Size Packed CRC32 Modified
266601 236758 11% 20916587 Jan 11 2018 09:58 etc/JanosClasses.jar
1 files listed
bruce_dev />
bruce_dev /> zip -vl test.zip
verifying: etc/JanosClasses.jar (compressed)
1 entries found - content verifies!
bruce_dev />
I know that 24 seconds for 1/4 megabyte file is nothing to write home about. Now that things are fully functional I can go back and work on the LZ77 where basically all of the time is consumed. I can certainly improve on this performance but as is is, it isn’t that bad. The JNIOR is a controller after all and you likely wouldn’t need to compress other archives.
